What is the point? The point is to do math, or to dazzle friends and colleagues with advanced statistical techniques. The point is to learn things that inform our lives. - Charles Wheelan [PREFACE: I purchased Naked Statistics by Charles Wheelan many years ago, thinking its an important book to add to any Math Teacher’s arsenal (and it is!) but had only gotten through the first three chapters before dismissing it for another read. It is not a boring book - quite the opposite in fact - but I felt that mere passive reading was not enough for me to really retain the important ideas and intuition that Wheelan is trying to impart to his readers. This time, I’m giving it another chance and plan to summarize material I am learning, relate it to my own experiences, and share that learning here on my blog.] I wrote about why statistics matters in a previous post. Here, I continue to elaborate on the point as I summarize my biggest takeaways from the first chapter. This chapter provided an overview of big ideas in statistics that we’ll be learning about throughout the book. Description and Comparison Descriptive statistics is like creating a zip file, it takes a large amount of information and compresses it into a single figure. This figure can be informative and yet completely striped of any nuance. Like any statistical tool, one must be careful of how and when we employ such figures and the implications it might have on the audience. So a descriptive statistic is a summary statistic. Let’s start with one that many of you may already be familiar with - GPA. Let’s say a student graduates from university with a GPA of 3.9. What can we make of this? Well, we might be able to discern that on a scale from 0 - 4.0 a GPA of 3.9 is pretty darn high. But some universities grade on a scale of 0 - 4.3, accounting for a grade of A+. What this simple statistic doesn’t tell us is what program did the student graduate from? Which school did they attend? Did they take courses that were relatively easy or difficult? How does this grade compare with others in the same program? Wheelan writes, “Descriptive statistics exist to simplify, which implies some loss of nuance or detail (6).” Inference We can use statistics to draw conclusions about the “unknown world” from the “known world.” More on that later. Assessing Risk and Other Probability Related Events Examples here include using probability to predict stock market changes, car crashes or house fires (think insurance companies), or catch cheating in standardized tests. Identifying Important Relationships Wheelan describes the work of identifying important relationships as “Statistical Detective Work” which is as much an art as it is a science. That is, two statisticians may look at the same data set and draw different conclusions from it. Let’s say you were asked to determine whether or not smoking causes cancer? How would you do it? Ethically speaking, running controlled experiments on people may prove unfeasible, for obvious reasons. An example Wheelan offers here goes something like this: Let’s say you decide to take a few shortcuts and rather than expending time and energy into looking for a random sample, you survey the people at your 20th high school reunion and look at cancer rates of those who have smoked since graduation. The problem is that there may be other factors distinguishing smokers and nonsmokers other than smoking behaviour. For example, smokers may tend to have other habits like drinking or eating poorly that affect their health. Smokers who are ill from cancer are less likely to show up at high school reunions. Thus, the conclusions you draw from such a data set may not be adequate to properly answer your question. In short, statistics offers a way to bring meaning to raw data (or information). More specifically, it can also help with the following:
Lies, damned lies, and statistics. - Mark Twain
0 Comments
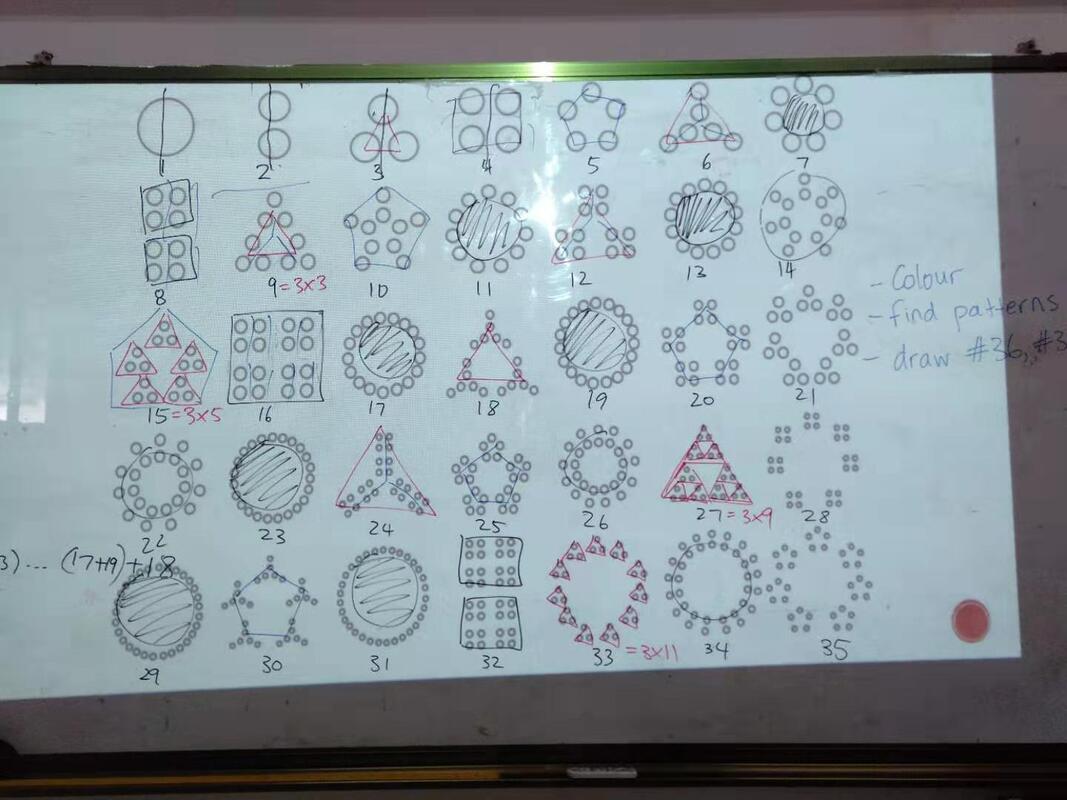
So I was lucky enough to have the opportunity to teach in the Head Start summer program at my international school here in China. The program is intended to help students going into high school to gain exposure to full English immersion classes in Math, Science, Socials, and Language Arts. I taught four blocks a day for 70 minutes each. Each class had anywhere between 12 - 16 students. Ten days straight; on the one hand, no break (kinda brutal), and on the other, open curriculum (YES! Free reign). I had lofty plans. I'd been refreshing myself on Jo Boaler's work about mathematical mindsets (see my previous ramblings here). I was going to do a little study. Please note that I do not have any experience whatsoever doing educational research. While I have a general understanding of the scientific method, I was mostly doing this out of pure curiosity and a desire to become a better teacher. Like all good mathematicians and in the name of good science, it was perhaps inevitable that first time was not the charm, and rather than have a very successful, replicable study, I instead gained some knowledge about how I might proceed in the future. Nice. Content that I had planned to cover in 10 days would have taken closer to 18. The students had an incredible range of English speaking ability, with drastically varied dynamics between groups of students. The schedule did not operate on a cycle, so I saw the same group of students at the same time each day, which definitely influenced their learning experience. For instance, Group C who were absolute angels and ready to learn each day in my first period class were exhausted by the time they got to third period, which led to more behavioural problems in the classroom. STUDENT DYNAMICS Group A: A challenging group. I saw them the period right before lunch each day and there was a group of four students who were unable to sit still and wandered the class during inappropriate times, such as in the middle of me giving instructions. I lost my cool on this group; shame on me because I wasn't able to regulate my emotions and respond calmly to the situation. Just to clarify, a "losing my cool" moment for me doesn't mean shouting or yelling, which is neither helpful nor productive. I simply raised my voice to get the students attention. But, in that moment, I had lost my cool because I let the students dictate my response rather than carefully assess the situation and respond calmly and accordingly. Group B: Did absolutely anything in their power to NOT pay attention. Would whine anytime I introduced a new activity. Would put their heads down and sleep in class. I saw this group after lunch each day, they were my last and perhaps most challenging class because of the incredible amount of sleepers and students who wanted to do absolutely nothing. There were definitely some gems in this class that would have benefitted from being in a group with other, more responsive students. Lots of patience and flexible teaching strategies required. Group C: The first group I saw each day and by far the best group. Students had a decent command of English and I rarely had to repeat myself. They would listen and follow instructions the first time. Students would always do as they were asked. The challenge with this group was pushing them to work slightly beyond their zone of proximal development. Group D: A diverse group with students who always wanted to be two steps ahead, students who needed a lot of personal assistance, students who got distracted easily, and students who were happy with just coasting along. HOW I COLLECTED DATA I used Boaler's Mathematical Mindset Teaching Guide as a self assessment tool for how I was and was not strengthening growth mindset culture in my math classroom. I wanted to focus on changing students' inclinations towards math learning, challenging those who believe math is a subject that defies creativity and passion, and pushing those who already saw themselves as "math" students to expand their definition of what math is. With the help of my math mentor, I settled on collecting data through a mindset survey. Students took a before and after survey. I added two prompts on the after survey that required students to provide written answers to the following: - What I think math is... - How math class makes me feel... A source of error here is that for students with low English level, they may not have fully understood the meaning of the statements they were agreeing or disagreeing with. Another possible source of error (though unavoidable) are those students who "did" the survey by randomly clicking boxes just to appease their dear teacher. HOW I TAUGHT I chose content from YouCubed's Week of Inspirational Math. I chose these tasks because they were all low-floor, high-ceiling tasks and were designed to build good mathematical habits of mind. For example, on day 1, we did an activity called "Four 4's" which encouraged students to think creatively and work collaboratively to come up with as many expressions as they can that equal the numbers 1 - 20 using only four 4's and any mathematical operation of their choice (see picture below). Other activities we did:
In terms of assessment, I wanted to stay as far away from tests or quizzes as possible. Instead, I focused on providing students with specific, written feedback on their journal entries, group quizzes, and one final presentation at the end. I wasn't concerned so much with what they knew, but rather the process through which they were learning and engaging with the material. RESULTS
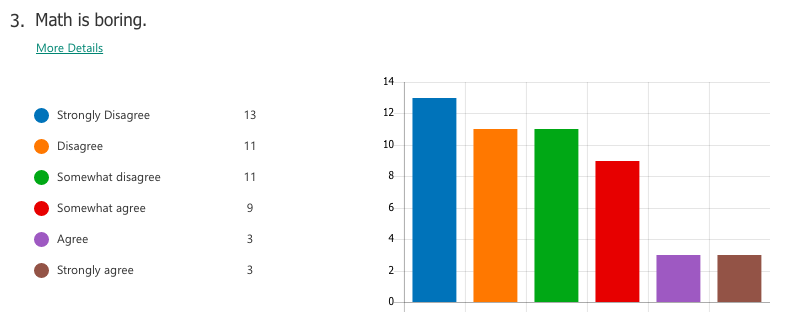
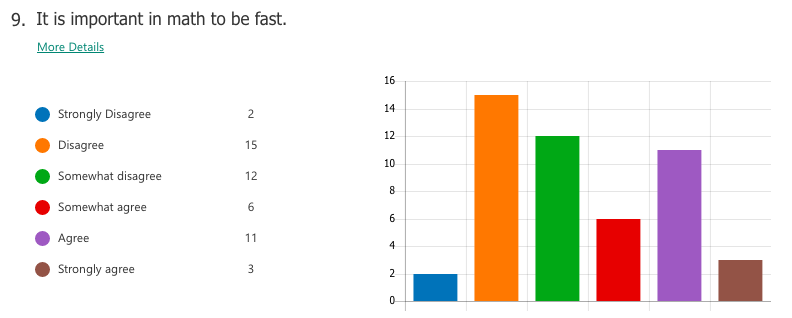
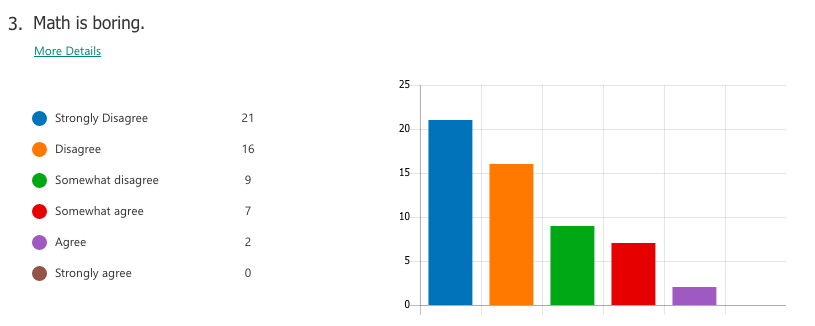
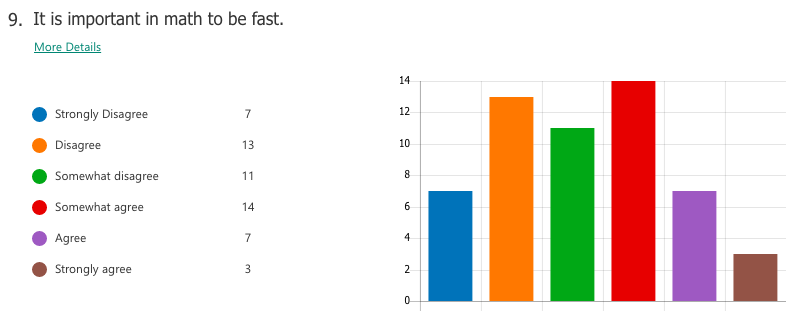
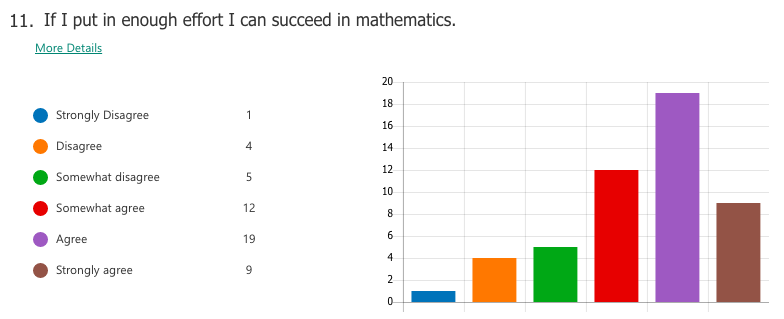
Select responses to "What I think math is"
"Interesting" "The most important things we need to learn" -"Have unlimited creativity" "Magic" "Subject between creative and and teamwork" "is very interesting. make my brain growing" "beautiful" "fantastic" "Math makes me hate and love" Select responses to "How math class makes me feel" "Better" "Moer interesting than chinese class" "It may not very interesting, but OK" "happy that I learned a lot" "I feel very good, I meet very good teacher also know the very good friend in the math class" "exciting" "I feel happy when I fiand the ancer" "free" "Good! make me more confedent" WHAT I LEARNED A majority of students already had tendencies towards a growth mindset in mathematics, perhaps as a result of the general high regard Chinese people hold for mathematics as a subject. For the most part, students liked math and saw themselves as capable of achieving if they worked hard enough. Of the 59 students I taught, a small number of students (three or four) were of the opinion that they were "just not math people" and were extremely hesitant in trying. In the end, I can't really say definitively which factors of my teaching influenced (or failed to influence) a stronger growth mindset towards maths. What I do know is that the switch to low-floor, high-ceiling tasks was extremely freeing -- for me and for the students. It allowed us to take a concept or idea as far as we wanted to go. There was no script or prescribed problem set that the students had to work through in increasing levels of difficulty, but rather a greater depth of thinking, and the time and space for that thinking to happen. Despite (or maybe thanks to?) the lack of testing (there were none), students still engaged with the tasks and content at high levels, drawing conclusions they might never have done with a pre-made worksheet of the skills they were supposed to practice. By building a stronger focus on increased depth of knowledge, it then follows that a necessary norm to advocate would be that math isn't about speed. When people refer to themselves as not "math people", that's usually what they refer to, the fact that they aren't fast at mental arithmetic. But math is so much more than that. In all, while it is hard to say from the students' perspective whether or not they appreciated a stronger switch to teaching with mathematical mindsets in mind, I know that for me it resonates as a noble endeavour. Yes, it is much easier to write a test and spend 70 minutes of your life making sure no one cheats. But take that same test, rip it up, and replace it with a diagram, an equation, a single question, a blank sheet... and possibilities begin to emerge. Some groups may reach a higher level of understanding and some may not, but then again, we teach students, not subjects. I recently attended a professional development session led by a colleague titled, "How to Make Any Worksheet into an Escape Room," which helped us experience an escape activity from the student perspective. It was the bomb. Dot com. The session touched on ideas expressed in this article, which happens to share the same title. Two weeks later, I ran an escape room in my classroom. It was the most fun I'd had all year. Cue intro. Goal: Answer the question, "what is life?" Other than that, I gave my students VERY little prompting. I figure I'd let all the mysterious new locks that had been placed in my classroom do most of the talking. In order to answer the question, they need to collect all four puzzle pieces, which eventually led to this: The escape activity was designed to work in a linear fashion, so students had to unlock each combination in sequence in order to get to the next clue. Clue 1: Integration Students were given a numeric code that had to be converted to a word after correctly solving the given integration problem. The answer was "SNACKS," which happens to be a location clue, leading to the refreshments centre where I provide students with water, tea, and snacks. The answer to the first clue was hidden under the snack basket. Many students got stumped at this point and wasn't sure what they were supposed to do (I didn't give them ANY other instructions). Once they got going, however, they really got into the flow of it. Clue 2: Derivatives Matching I used a matching activity here from Flamingo Math (teachers pay teachers) and students had to find the four digit number code based on the highlighted boxes. (So they didn't actually have to complete the entire matching activity). Clue 3: Find the Mistake The answer: Students convert correct answer into letter code to unlock the letter lock. Clue 4: Calculus Crossword The answer: Highlighted in invisible ink are the words TRIAL. A couple observations:
A great format for STEM OLYMPICSThe same colleague who lead the Escape pro-d was also part of the planning committee for our first ever STEM Olympics (shout out to my buddies Flower, Jeon, Im, Yin and Patel if you're reading!). ROUND 1: Unlock one of three boxes
ROUND 2: Gain 5 points in a trivia style tournament
 While it does take some time and planning, the escape room format is a great way to review and preview content for a unit or course. I like that it is completely student driven and there is a great deal of collaboration that happens. The novelty factor with the physical locks also played a great role in keeping students interested and engaged, although it is possible to adapt this activity to be completely digital (Onenote or Google forms).
Since then, I've created two other escape activities with my classes. They're a lot of fun to make and the possibilities for clues and questions are endless! This is definitely an activity I'm going to keep using in my classes. Never in my life did I ever imagine myself teaching in China, and yet, here I am for a second year at that! Below are images of welcome packages I put together for the members in the Math Department this year, which includes: - A door sign with the teacher's name, room number, and teaching schedule -Stickers, 'cuz duh -Coffee, a key element in sustaining the life force of a teacher -A pack of cards, essential in any math teacher starter kit -A math puzzle, fuel for the brain I'm super happy with the way they turned out, and I'm looking forward to a good year ahead! This year I'll be teaching Pre-Calculus 11 and Calculus 12, which I'm both excited and nervous about! It's been years since I've taken Calculus and this will be my first year working with twelfth grade students (I've been doing a lot of review this summer on Khan Academy). Here's a fun activity that I found on Kate Owen's blog that I plan on using this week with my Calculus 12 students. It's a great way to review concepts and vocabulary from Pre-Calculus to see what students already know and remember from the course. I've added some modifications and created an accompanying PPT that's a full lesson, all ready to go. Scroll down below to access this resource :) I'm a big believer in sharing teaching resources for free, and this is my way of giving back to the online teaching community that has given so much to me. Huge shout out to everyone in the #MTBoS, I love this community. The activity works as follows: 1.Students it with a partner, shoulder to shoulder. 2.One person faces the board, the other person faces away. 3.The person facing the board will be the explainer. 4.The person facing away will be the grapher. Warm Up: Teacher does warm up round with the students, describing a basic graph (ex. linear function) and students attempt to draw it in their notebooks. Discuss: What prompts were useful? Is there something the teacher said that could have made it easier? The Activity: (see above) Exit Ticket: Given a picture of a graph, students are to write a description that matches it in as much detail as possible. Extension: Students draw a graph and write a corresponding description. Scramble the results and have students match them!
Oh Polynomials. My least favourite unit by far in the Foundations of Math and Pre-Calculus 10 course I am teaching. Find the greatest common factor, least common multiple, factor these trinomials, collect and simplify like terms, the swimming pool has a width of 5x + 1 and a length of x + 2… YAWN. The ChallengeHow can I frame a boring, completely algorithmic and skill-based unit into something that's relevant and meaningful for my students? I am borrowing Dan Meyer's definition for relevance here. It Begins with a Question… A colleague asked me today, "How much time do you have for homework at the end of class?" This was a surprising question to me, and as I thought back over the 10 day unit, my answer was almost none. The question sparked a great dialogue between us about our approach to teaching the same content in our respective classrooms. It really made me think. I realized that while I still dreaded teaching polynomials, I had found a way to improve the way I taught it from first semester that required less rote work and more thinking. One thing that has not changed, however, is that I avoid teaching FOIL method like the plague. It only works for expanding binomials and does not apply for polynomials with more than two terms. After I read this article I was convinced I would never need FOIL in my classroom: http://www.makesenseofmath.com/2016/11/why-i-will-never-teach-foil.html For a good laugh: https://saravanderwerf.com/2017/04/01/why-ive-started-teaching-the-foil-method-again/ Some things that came up in our discussion:
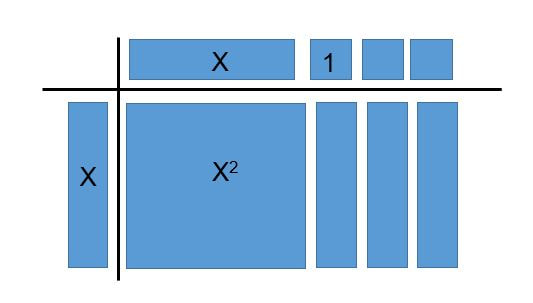
1. Algebra Tiles Definitely a hate-hate relationship. As a math teacher, I am obligated to entertain this idea and I do admit it has its benefits, especially in lower level math classes when students are initially being exposed to distributive property and the like. The problem, however, was that my students were already armed with the skills and knowledge of multiplying and factoring polynomials. Moreover, the limitations of using tiles far exceeded the benefits, in my opinion. Algebra tiles do NOT work for: polynomials higher than degree two, multiplying more than two polynomials, and multiplying polynomials with more than three terms. This meant that it took more effort for students to understand how and why it works. Nevertheless, we spent a few classes examining algebra tiles and their usefulness. Rather than approach it from the typical standpoint of using algebra tiles as a manipulative, I wanted students to see the link between the algebraic and pictorial representations of polynomials. This took work and was not as straightforward as it seemed. A big takeaway for me was that students gained much more out of the experience when they were able to physically manipulate the tiles and arrange them into their "factored forms." Last semester, I "taught" algebra tiles by merely showing them examples and drawing them on the board. It took a bit more prep, but this semester I printed eight sets of tiles (positive and negative) in my classroom and had students manipulate them instead. If we were to spend any more time on the unit, or if this was a lower grade level, as an enrichment activity I would have students discuss the limitations of algebra tiles and look for ways to address them. 2. Picture TalksI like to use Sarah VanDerWerf's Stand and Talks as a format for students to discuss picture prompts. I find that the buy in for engagement is much higher when the prompt is linked to physical movement. My favourite questions for photo prompts are: "What do you notice?" and "What do you wonder?" What are my photo prompts, you ask? That's right. Algebra tiles. Goals for students:
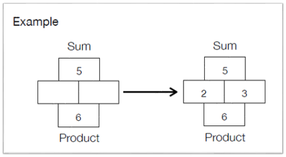
I like this activity because it is easy to differentiate and works well as a "minds on" for any topic. Asking students a general question like what they notice/wonder means that lower ability students can comment on ANY aspect of the photo (e.g. "there are blue and green rectangles") while higher ability students can be pushed towards making observations based on any mathematical patterns or relationships they observe (e.g. "the green tiles represent positive polynomials and red tiles are negative"). 3. Factoring Method - Criss Cross or Sum Product?I've had the great fortune of only having one prep and a spare block this semester (for friends and readers who don't teach, that's teacher jargon for FREE TIME, kinda. The details are not important). Anyway, I've been making drop-in's to my fellow colleagues classrooms with my new-found "free time" and one thing I picked up was the importance of proper SEQUENCING. For instance, a natural progression for factoring trinomials might look as follows:
That, together with a quick exercise on sum/products, helped me push students towards seeing the relationship between the factored form of a trinomial, and the sum/product method. I prefer this method over the traditional "criss cross" method for a few reasons
Which One Doesn't Belong? (WODB)Fantastic activity for building up thinking skills and vocabulary. Each student picks one of the expressions and must argue why that one doesn't belong. Benefits:
Sample answers: "27x^2 doesn't belong because it is the only expression that has a coefficient with a perfect cube" "45x^2 doesn't belong because it is the only expression that has a coefficient with 5 as one of its prime factors" More WODB prompts can be found here. Taboo How it works: One student is chosen to stand/sit at the front of class facing the audience, they are in the "hot seat". Behind them, a vocabulary term is shown for the rest of class to see. Students in the audience must help the student in the hot seat guess the vocabulary word by miming, explaining the definition, or giving examples. They may not use any part of the word in their explanation. Modifications: Differentiate by giving students the option of bringing a "cheat sheet" of vocabulary terms with them. Prepare students for the activity by giving them cross word or fill in the blank exercise reviewing the vocabulary words for the unit. An "expert round" can include vocabulary not on the cheat sheet. "Challenge round" can be facing a peer or the teacher. Can play in teams or as a class. Human Bingo
his activity was shared by a good colleague of mine. To get BINGO, students must find one "expert" in the classroom to answer each question on the bingo card until all the questions have been answered. The student who answers the question must sign their name. A student may not be asked more than once to answer the same Bingo card.
Benefits:
Semester one of my first year living and working in China is officially over! Since my last post about the first day of school, I realized haven't blogged at all this entire semester. I am a little disappointed that I had skipped through all the middle bits, but regardless, here we are.
This past semester I taught Math 10 and 11 of the British Columbia curriculum at an international school in Suzhou, China. With the exception of a handful of students, all of them are English Language Learners. Some might argue that this does not pose a big problem in mathematics, since the language of mathematics can be viewed as a combination of abstract signs and symbols separate from the English language. The problem is, it is one thing to understand mathematical ideas and concepts, but another to be able to communicate them. Someone who is well versed in a mathematics should theoretically be able to describe the same concept in more ways than one - numerically, algebraically, graphically, and verbally. Mathematicians strive for precision in expressing ideas, and this is not always simple. Aside from students having to approach mathematics from an ELL standpoint, the issue is compounded when you consider all the ways in which ambiguity arises in the English Language. Take for instance the word "and"; conjunction in mathematics is commutative (A^B is the same as B^A), but you can see from the example below that "and" in everyday English is not commutative. The sentence, "John took the free kick, and the ball went into the net," would have a very different meaning if the conjuncts were reversed (Devlin, Introduction to Mathematical Thinking). For my most challenging students, the issue wasn't so much as getting them to communicate their mathematical ideas well, but getting them to communicate at all. For students with extremely low level English ability, being afraid to speak or ask questions in class was a huge roadblock in developing a good grasp on the mathematics we aim to study. The most frustrating times were when students didn't even bother to try. Perhaps this has something to do with being in a culture where "saving face" is important, but students were sometimes so afraid of being wrong that they left entire test pages blank, multiple choice even! (Yes, I know, I was stunned!) You've probably heard this a million times but I'll say it again, mathematics is not a spectator sport! You have to do it to get it, like riding a bicycle. (Am I preaching to the choir here?) My biggest goal this semester is to get students talking more. About mathematics. In English. A large part of my success will depend on how well I set up a classroom culture of trust and acceptance. This is huge. If I have any hope of getting students to share their original thoughts and ideas they need to know they are safe doing so. Luckily, I've got some ideas to help me get started, but the rest will be trial and error (as is most of my teaching anyway). I also plan on working in a slower progression at the beginning of the year to first get students acquainted with some of the language used to describe mathematical expressions before we dive into what exactly mathematics is. With any luck, every student will be able to describe, in English, what we are learning in any given unit. Things That Went Well in Semester 1 1) I finally found a groove! Lesson planning no longer takes up hours and hours each day (#win), and I also have a nice support network of experienced teachers to draw ideas from and borrow resources from. Establishing daily routines early on in my classroom (and enforcing them!) also worked wonders. 2) Brain breaks. I was a little hesitant about these at the start since they seemed silly and unnecessary if the lesson is well-chunked. I learned early on though, not all lessons are made equally and some days really are a drag, especially when are teaching 80 minute blocks. Taking a short 5-10 minute break to stretch/play a game/go on your cell phone provides both myself and the students some much needed refuge from a long period of work. 3) First week activities. As I mentioned earlier, setting up a warm and inviting classroom culture is key to being able to get students to talk more math, and learn more in general. I spent about a week doing activities and playing games related to math with my students last semester before I started diving into teaching any curricular content. I plan on spending about the same amount of time, if not more, this coming semester settling in with my new classes. Lesson Theme: Introduction to Probability and Counting Prerequisite Knowledge: Permutations and Combinations Here's an activity that I introduced to four groups of tenth graders in a recent unit on probability:
Provide minimal guidance as the groups decide on the number of combinations for each scenario. I made an exception for students who asked clarifying questions, such as: - Are there any repeating digits? - How many digits repeat? The hints are open to interpretation on purpose in order to get students thinking about the sorts of constraints they would need to consider when calculating the total number of outcomes. The discussion phase of the activity provided a rich opportunity to address student misconceptions about permutations and combinations, as well as the importance of reasoning, i.e. Does this number make sense? Is this estimate too high or too low? How does this number compare with my initial guess (intuition)? What if there were no constraints, what would the answer be? The Solutions: TEAM GARRY - 3 digit code, repetitions allowed. This hint is not much of a hint at all. "Repetitions allowed" could mean that there may be or may not be any repetitions in the code. So, one possible answer is simply 10 x 10 x 10 = 1000. There are ten ways of picking the first, second, and third digits. TEAM ORVILLE - 3 digit code, no repetitions. This narrows the playing field a bit. 10 x 9 x 8 = 720. Ten ways to pick the first digit, only 9 choices left for the second, then 8 for the third. TEAM APRIL - 4 digit code, numbers 2 and 3 appear in the code. (a) This would be significantly easier if the ONLY numbers in the code were 2 and 3. There are only 4 possible combinations, which are easy to figure out by hand: {2323, 3232, 2233, 3322} or 4!/ (2! x 2!) = 4. (b) With repetition. There are 4 ways of positioning the "2" in a four digit combination. For each way that the "2" has been positioned, there are 3 ways to position the "3." In total, we can arrange the digits "2" and "3" in 4 x 3 or 12 ways. If repetition is allowed, the total number of combinations would be 12 x 10 x 10 = 1200. (c) Without repetition. Similar to above, except that once we have found a placement for the "2" and "3", there are only 8 and 7 digits left to choose from respectively. The final answer would be 2 x 8 x 7 = 672 My notes and observations:
For reasons I still do not fully understand, my grade 10 classes were combined with another teacher's classes today. Classes are 80 minutes each, and are split up into two 40 minute blocks. I spoke to the teacher of the other group beforehand, and from what I could tell from her limited English (and my non-existent Kazakh), it seemed like we would each teach a 40-minute lesson to the combined classes. It was not until the lesson began that I realized this teacher wanted her group to work separately from mine. The lesson ended up being a disaster, a huge flop, an extreme "UGH" moment if you will, and one that I'm not too proud of. It felt like I was trying to teach against a storm. I felt disrespected by the other teacher and students in the room because they were being extremely noisy while I was trying to get through my lesson. I asked them to quiet down a couple times but then the noise level would eventually go up again. Thinking back, I wish I had been more adamant on insisting that I kept my classes and never combined groups in the first place. Again, for reasons I cannot explain, it seemed imperative to the other teacher that we kept the two groups together. So by the time my second class came along, I devised a new plan. I was better informed the this time around. I knew I had to share the same physical space with the other teacher and her students, and I knew that there would be at least minimal amounts of talking. I also knew that I didn't want to enter in a shouting match with the other class (fighting fire with fire just makes a bigger fire). Instead, I tried my hand at silent teaching. I left the following note up on the board for my class at the beginning of the lesson: The Results - What Worked: The silent teaching definitely got the students' interest and forced them to keep an eye on the board so that they could keep up with what was going on. A few students got the idea and were able to explain verbally what I was trying to do non-verbally - and English is their third language! (So proud!) The other class was noticeably more quiet this time around, and without me having to go into a shouting war with at least a dozen other voices, the noise level was much lower in general. I also noticed that some students from the other class were intrigued by what we were doing on the board, and stopped to observe our lesson. Once all six trigonometric proofs were finally complete, I gave a dramatic pause, and POOF - I got my voice back! What Didn't Work:
The students who are less visual were really craving verbal explanations. While classmates volunteered to help explain concepts to those who didn't understand the first time around, two students told me that they still felt really confused after the lesson. I wish I could find a way to make this a less teacher-centered lesson, and create more opportunities for students to get involved. I did call a couple of students to the board once I felt they got the general idea of the proofs, but I was not able to assess all my students one-on-one. An exit slip would have been useful had time permitted. Next Steps: I'll try my hand at silent teaching again in the future, but I'd like to find ways to create even more student involvement. Our topic this time was the sum/difference identities for trigonometry and it was very theory-heavy. Next time I think a topic (or even short demonstration) that is more straightforward to understand will be more effective with this teaching strategy. Also, I resolve to make facial expressions more dramatic for a fuller effect! Other Notes: I later realized my big dramatic moment at the end wasn't as dramatic as I had hoped. I called a student up to the board to complete the last proof, and it wasn't until after I "regained my voice" that I realized there was a major sign (+/-) error!  Here are two interesting questions I posed to my students in our unit on the transformation of shapes. (1) Playing card (on right): Where is the line of symmetry? I handed each pair of students a printout of the king of hearts and asked them to identify the line of symmetry. (2) M.C. Escher (below): Is this drawing symmetrical? Why or why not? It may be a good idea to preface both of these questions with, "What is symmetry? Give an example to support your answer?"
tedious, and it gives me some time to respond to all their entries. I try to vary the writing assignments as much as possible to add interest to the lessons, and students are encouraged to include pictures or diagrams to support their explanations.
The Solution: Both the above questions are meant to test how well students understand the idea of symmetry. Symmetry is any transformation that leaves the original shape or object unchanged. (1) In the playing card example, students often say that the line of symmetry is horizontal, vertical, or diagonal. In fact, there is no line of symmetry - as that would indicate reflective symmetry (mirroring an image). The type of symmetry exhibited on a playing card is rotational symmetry by 180 degrees (or point symmetry), meaning that you can cut the image in half at any angle through the centre of rotation, and the two halves will look exactly the same upside down. (I actually got my students to cut their playing cards in half at different angles to illustrate this property). (2) Most students are likely to state that the drawing does not exhibit any type of symmetry at all. Again, students at this stage tend to be familiar only with the idea of reflective symmetry. I will accept their answer as long as they provide a suitable justification. However, what I'm trying to get across with this question is that tessellations (translating an image/object) are a type of symmetry also. This creates a nice lead in to further discussion on geometry as it relates to art, or vice versa. Here are some teaching notes on a recent lesson I did on inverse functions with my group of grade 10 students. Learning Objective: Understand the definition of inverse functions and their relevance to everyday life. 1. Setting the Stage with Office Supplies Beginning the day's lesson with a "picture talk" can be a good way to get students to practice using subject-specific terminology. The pictures can be controversial, or you may choose to pick analogies relating to the topic of discussion, like the one below for instance. I find that leaving the questions open-ended gives students more freedom to get creative with their answers. A series of open-ended questions you might ask: What do you notice about this photo? What do you think 'x' represents? Predict: How do you think this photo relates to our new topic? Teaching Notes: A lot of my students like to shout their answers out loud when they get excited about a topic, which tends to drown out the quieter students and does not give them enough time to think. But sometimes, I get excited too and I basically just end up shouting “YES!” while enthusiastically pointing and staring wide-eyed at the students who yelled out the answer I was looking for. "The answer I was looking for" - which meant ignoring all other answers that may have added important insight to our discussion. Such habits are dangerous because they tend towards a classroom environment in which it is not safe to take chances or make mistakes. When I dismiss wait time and only acknowledge the quick answers, I am effectively giving everyone else the permission to shut down and stop thinking. To combat the issue of the shouting-the-answers-out-loud thing, I introduced this image by inviting students to take ten seconds (any more and they would have shouted the answers anyway) to silently look at the picture and gather their thoughts about it. When ten seconds had passed, I asked them to share their ideas with the person sitting next to them when they were ready. 2. Lesson Objective and the Enigma Machine By now, it is likely that students have guessed that the lesson has something to do with "functions" and "opposites." At this stage, I presented the day’s lesson objectives and key terms (with translations), along with a dashing photo of Benedict Cumberbatch in “The Imitation Game.” I gave a brief synopsis of the events in history in which the movie is based, and explained how it related to our topic of inverse functions. In retrospect, I probably should have posed this as a question instead: "How do you think this relates to our topic?" 3. Intro to Cryptography Next came the fun part, and what formed the bulk of the lesson. The students worked pairs and were asked to decode a hidden message within a twenty minute timeline. The less hints you give, the more challenging the activity becomes. (You can download the activity page along with my teaching notes below). Once the twenty minutes are up, you’ll see some students scrambling to finish decoding the message. Debrief the activity with them. Discuss strategy- for instance, how were they able to determine the cipher? Follow up- how do you think Alan Turing and the British Intelligence were able to crack the unbreakable code? (May choose to show video clip of the relevant scene in the movie for dramatic effect). Extension- What is the probability of randomly guessing the code correctly? What assumptions do you have to make in order to do so? (Can also relate topic to permutations and combinations). Teaching Notes: I downloaded a 20 minute digital countdown timer and added it to my ppt so students can keep track of how much time they had left for the task. If you have any English Language Learners in the class, it may be helpful to post the English alphabet on the board as an added hint. 4. Consolidation I ended the lesson by asking students to write a short journal entry relating to the picture shown at the beginning of class. I think a better journal prompt would have incorporated a debriefing of the cryptography activity. The students' journal entries gave me individualized feedback on how well they understood inverse functions and the composition of functions. A common mistake I noticed was mistaking the concept of reciprocals with inverse. Some students wrote that 2 and ½ were "opposites", and therefore the inverse of each other. Something to address in my next lesson. My lesson on permutations was inspired by this post by Dan Meyer. I teach a group of very bright and mathematically inclined students at our school. While my students' computational abilities and mathematical knowledge are almost second to none, a majority of them tend to lack skills of inquiry and critical thinking. This is due to the fact that the curriculum is dense and completely knowledge driven, which leaves little opportunities for linking (making connections) or creativity. I believe the second culprit of this phenomena is the post-Soviet style culture and traditions in which the Kazakh education system is rooted. I see that my colleagues are under constant pressure to deliver heaps of content from a prescribed curriculum which is flawed to begin with. To provide some context, one term is roughly 6 weeks long. In those six weeks, we typically cover three units of work, with a prescribed 12-16 hours of teaching per unit. The end of each unit is followed by a formative assessment (1-2 hours). This leaves 10-14 hours of actual instructional time, of which is no where near enough time to cover all the topics we need to cover AND engage students in meaningful inquiry-based projects. As a result of the limited time constraints, we are basically teaching one new concept a day. The students, meanwhile, are left to soak up as much as they can (like sponges that retain very little water, or knock-off expandable water toys that actually stay the same size) before the end of term summative. Add to this the other 7-10 classes the students are required to take, and you can see the students have an enormous workload. They are in school six days a week, at least 9 hours a day. There's just no time! The default solution? LECTURES. There aren't many opportunities for engaging students in rich learning tasks, but I try to squish in bits of it whenever I can. As I said, my students are extremely gifted but are used to thinking in terms of algorithms and formulas, so I often get a lot of blank stares and a lot of "Why are we doing this?" when I engage them in conceptual thinking - which is exactly the point! "Why ARE we doing this?" I ask, and that really grinds their gears! Slowly but surely, the students are getting used to this rather "oddball" tendency of mine (in their p.o.v.) to turn things around put the onus of learning on them. And golly I think it's working! So anyway, here's how I began our unit on Combinations: I placed students into groups and organized a placemat activity. Instead of me asking the questions, I wanted to know what opportunities the students saw when looking at this picture. Some answers they came up with (no modifications made): - How much combinations can be made sum of digits in each number is 53? - How much combinations do we have if key consist of 3 digits? - What is the possible length of the hardest password? - How many possible variation of making code with all numbers (all numbers can be used one time, and must be used)? - How many numbers that password include? - What is the probability of randomly unlocking the lock? - How many explosive charges are required to blow it? As I ponder this list I see a rich minefield of opportunities before me. Within a five minute brainstorming session, my students touched on permutations, probability, and of course, "real-life" problems. I put "real-life" in quotations here because I believe the relevance of math to everyday life is relative. My version of "real-life" is different from my students, and I certainly don't expect all my students to be making calculations with factorials on an everyday basis. I was blunt with my students, though I certainly didn't mean to be... it sort of just slipped out. "Some of you might never use this again in your lives," [cue snickering, whoops], "but..." There's always a "but" of course, and I'll leave it to you and your imagination to fill in the rest of the sentence. Once the snickering subsided, I proceeded to introduce factorial notation. The sequencing worked out beautifully because once the students were familiar with factorial notation, we revisited the lock picture and the students were able to derive the formula for permutations themselves! All I did was ask "How many possible combinations are there?" and students were quickly able to discover that we needed to define more parameters in order to answer the question. E.g. How many digits are there in the code? Can numbers be repeated? Beautiful! At the end, I gave them the following exit questions: 1. Define permutation, in your own words. 2. Give an example (not used in class) of a permutation problem. I was surprised at some of the responses I got. First, I learned that the class had a diverse understanding of the word "permutation" (I never actually gave them a definition), so now I know where the gaps in my teaching were. Second, not only did their examples show me the depth at which they understood the topic, but some students were able to accurately predict the types of questions we would be covering in future lessons. So instead of using textbook questions, we can explore the ones they came up with in class. Brilliant! “I teach high school math. I sell a product to a market that doesn't want it but is forced by law to buy it.” — Dan Meyer |
April SooInternational math educator who writes, occasionally. Archives
April 2020
Categories
All
|
||||||||||||||||





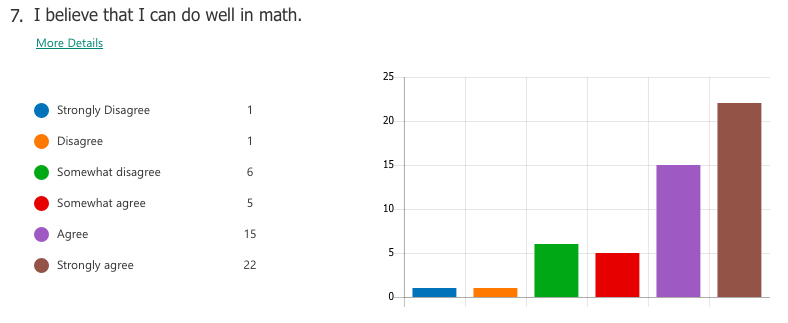
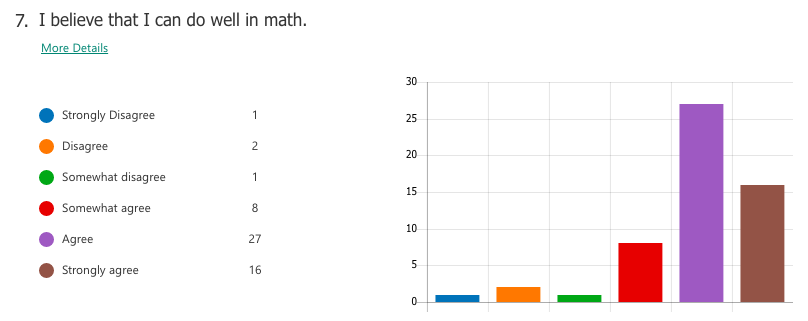
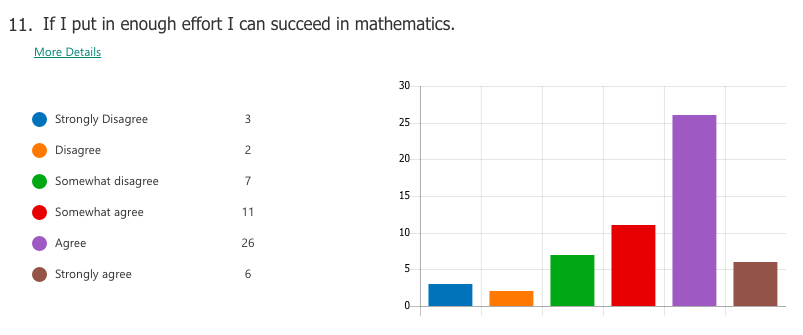
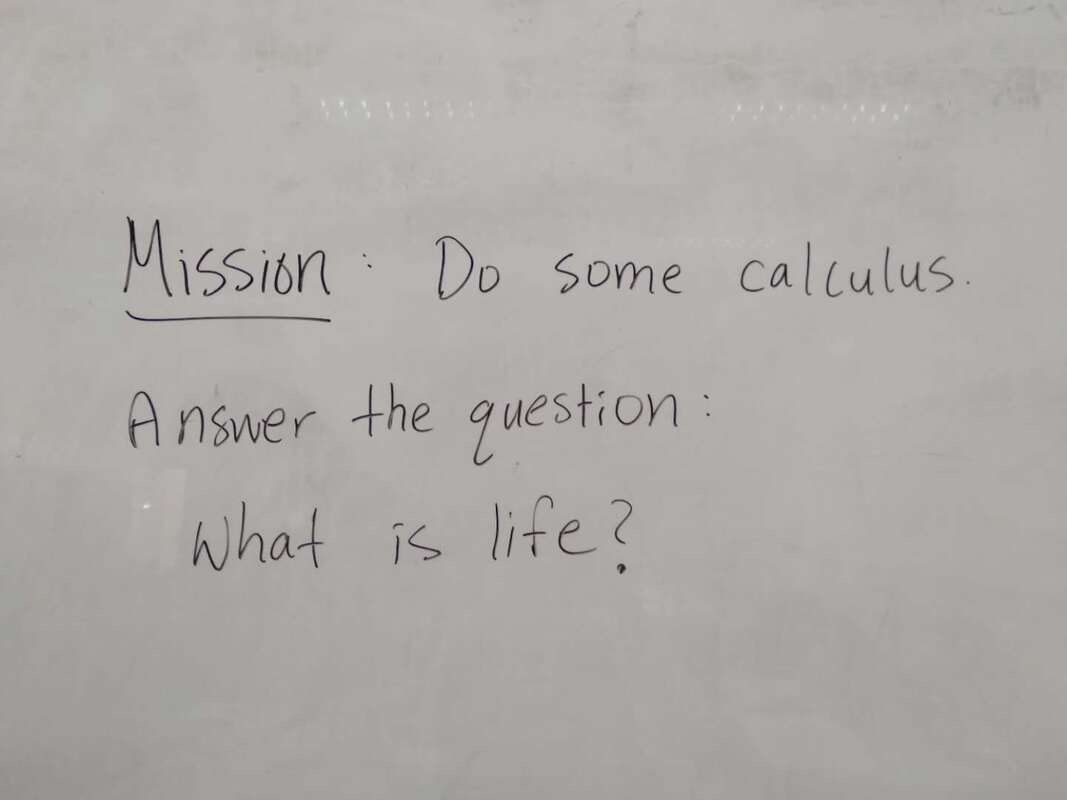





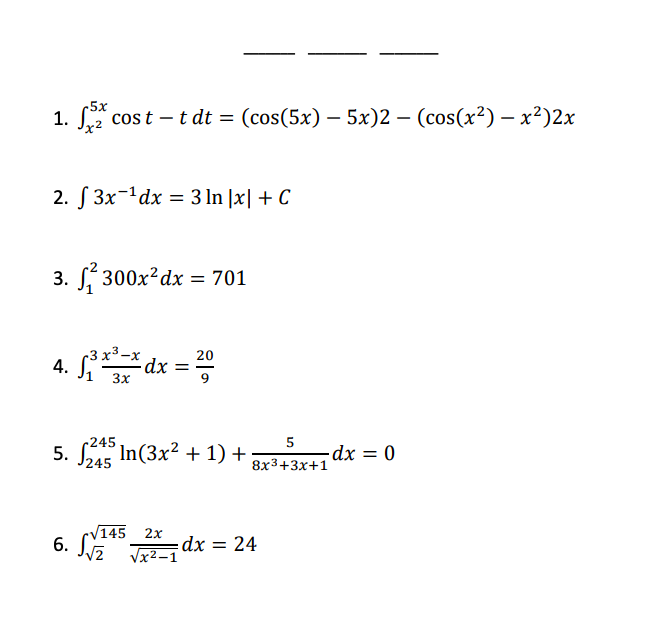










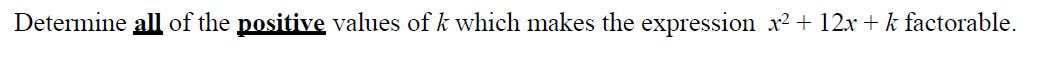


















 RSS Feed
RSS Feed
