|
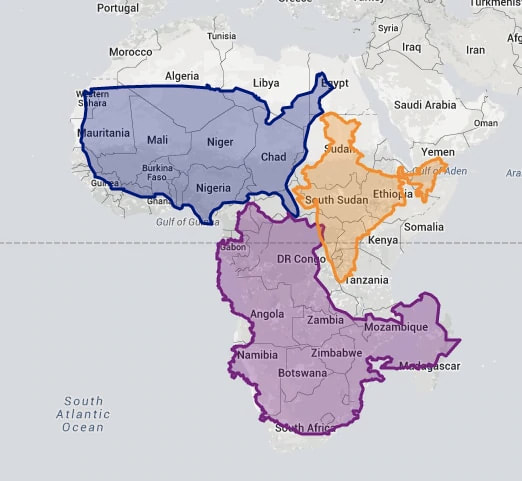
We've been looking at map projections for my masters course and I continue to be blown away by how embedded mathematics truly is in our every day lives. As a self-identified directionally-challenged individual, geography and anything like it is to be avoided at all costs. I find myself at my wit's end now and have to admit that even maps hold a lot of mathematically intriguing ideas that are worth exploring. The course I'm taking now is called "Math for Global Citizens", offered at the University of Waterloo to MMT students, taught by Judith Koeller and is arguably one of my favourites in the program. The problem of the "flat earth" has been around for centuries. It is believed that as early as the year 354, pre-medieval scholars asserted that the earth was in fact spherical (University of Waterloo). The problem for map-makers, then, is to find a way to depict a spherical object on a 2D surface, and this is turns out to be an impossible task. Take a look at the animation below for what's called a "Myriahedral projection" developed by Jack Van Wijk from the Netherlands. The idea behind a "Myriahedral projection" is to split the earth up into polygons, thousands of them, in order to preserve both shape and size of major land masses or bodies of waters (see article here). Map projections have not always been so advanced however. In trying to depict a spherical surface onto a 2D plane, one can try to preserve distances, shape, areas, or shortest distances between points by straight lines. It is impossible to have all these desirable properties in one map. For instance, the Mercator projection map is the one that we are probably all most familiar with as it preserves angular distances, making it easy for navigation, but it drastically skews areas the further away the land masses are from the equator. See this true size (thetruesize.com) comparison below, showing how large the continent of Africa actually is compared to the US, China and India: On that note, I would highly recommend checking out thetruesize.com and just playing around. Here's another great video explaining "Why all world maps are wrong" that was recommended to me by Mr. Schwartz, a geography teacher and the humanities Department Head at my school.
0 Comments
What is the point? The point is to do math, or to dazzle friends and colleagues with advanced statistical techniques. The point is to learn things that inform our lives. - Charles Wheelan [PREFACE: I purchased Naked Statistics by Charles Wheelan many years ago, thinking its an important book to add to any Math Teacher’s arsenal (and it is!) but had only gotten through the first three chapters before dismissing it for another read. It is not a boring book - quite the opposite in fact - but I felt that mere passive reading was not enough for me to really retain the important ideas and intuition that Wheelan is trying to impart to his readers. This time, I’m giving it another chance and plan to summarize material I am learning, relate it to my own experiences, and share that learning here on my blog.] I wrote about why statistics matters in a previous post. Here, I continue to elaborate on the point as I summarize my biggest takeaways from the first chapter. This chapter provided an overview of big ideas in statistics that we’ll be learning about throughout the book. Description and Comparison Descriptive statistics is like creating a zip file, it takes a large amount of information and compresses it into a single figure. This figure can be informative and yet completely striped of any nuance. Like any statistical tool, one must be careful of how and when we employ such figures and the implications it might have on the audience. So a descriptive statistic is a summary statistic. Let’s start with one that many of you may already be familiar with - GPA. Let’s say a student graduates from university with a GPA of 3.9. What can we make of this? Well, we might be able to discern that on a scale from 0 - 4.0 a GPA of 3.9 is pretty darn high. But some universities grade on a scale of 0 - 4.3, accounting for a grade of A+. What this simple statistic doesn’t tell us is what program did the student graduate from? Which school did they attend? Did they take courses that were relatively easy or difficult? How does this grade compare with others in the same program? Wheelan writes, “Descriptive statistics exist to simplify, which implies some loss of nuance or detail (6).” Inference We can use statistics to draw conclusions about the “unknown world” from the “known world.” More on that later. Assessing Risk and Other Probability Related Events Examples here include using probability to predict stock market changes, car crashes or house fires (think insurance companies), or catch cheating in standardized tests. Identifying Important Relationships Wheelan describes the work of identifying important relationships as “Statistical Detective Work” which is as much an art as it is a science. That is, two statisticians may look at the same data set and draw different conclusions from it. Let’s say you were asked to determine whether or not smoking causes cancer? How would you do it? Ethically speaking, running controlled experiments on people may prove unfeasible, for obvious reasons. An example Wheelan offers here goes something like this: Let’s say you decide to take a few shortcuts and rather than expending time and energy into looking for a random sample, you survey the people at your 20th high school reunion and look at cancer rates of those who have smoked since graduation. The problem is that there may be other factors distinguishing smokers and nonsmokers other than smoking behaviour. For example, smokers may tend to have other habits like drinking or eating poorly that affect their health. Smokers who are ill from cancer are less likely to show up at high school reunions. Thus, the conclusions you draw from such a data set may not be adequate to properly answer your question. In short, statistics offers a way to bring meaning to raw data (or information). More specifically, it can also help with the following:
Lies, damned lies, and statistics. - Mark Twain
It’s easy to lie with statistics, but it’s hard to tell the truth without them.  [PREFACE: I purchased Naked Statistics by Charles Wheelan many years ago, thinking its an important book to add to any Math Teacher’s arsenal (and it is!) but had only gotten through the first three chapters before dismissing it for another read. It is not a boring book - quite the opposite in fact - but I felt that mere passive reading was not enough for me to really retain the important ideas and intuition that Wheelan is trying to impart to his readers. This time, I’m giving it another chance and plan to summarize material I am learning, relate it to my own experiences, and share that learning here on my blog.] A couple of days ago, my younger brother, who just started his first year in university in the Fall, was complaining to me about the woes of student life; in particular, the obsession with grades and the paradoxical lack of willpower to work for them. Having taken an accounting class together, his friend recounted to him that it was, “The sketchiest 90 I ever received.” Let’s break that down for a moment. Humble brag? Yes, but what he really meant was that his friend was blindly memorizing formulas, plugging and chugging without any idea how they were derived and why they are meaningful. Does that sound familiar? How many of you have had similar experiences in math class? I know I have. Not just math, but in science, language arts, history… sometimes it feels like we are just memorizing facts in isolation without an understanding of their greater purpose. To be fair, I’ve taken statistics classes that feel no different, a series of formulas that need to be applied to raw data. What makes statistics inherently different, however, is that unlike calculus or algebra courses, which often teach skills in isolation of their applications (to which I will argue there is intrinsic value in knowing and learning, another post perhaps) statistics IS applied mathematics. Every formula, number, distribution test...etc. is meant to clarify and add meaning to everyday phenomena (though, when wielded improperly, can have the opposite effect). Statistics are everywhere - from which are the most influential YouTubers, to presidential polling to free throw percentages. What I love about this book is that it focuses on building intuition and making statistics accessible to the everyday reader. A quote by Andrejs Dunkels shared by the author, “It’s easy to lie with statistics, but it’s hard to tell the truth without them.” |
April SooInternational math educator who writes, occasionally. Archives
April 2020
Categories
All
|

 RSS Feed
RSS Feed
