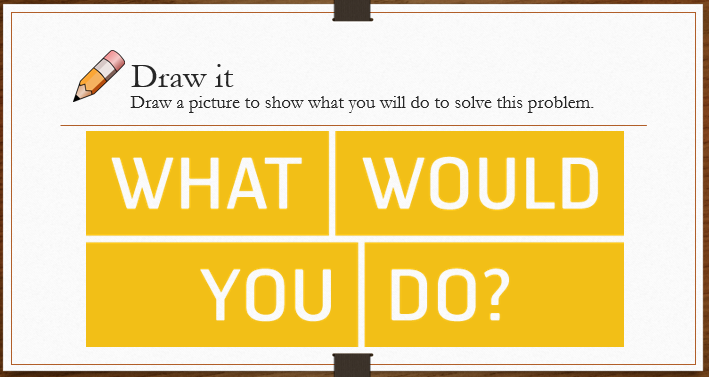
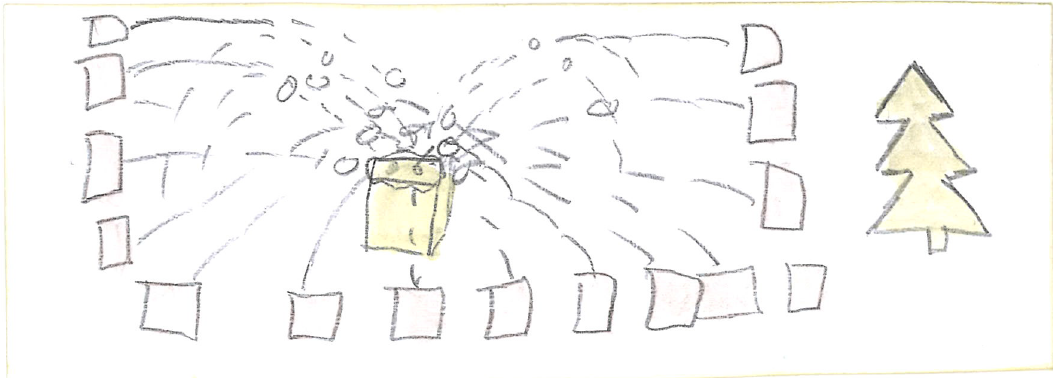
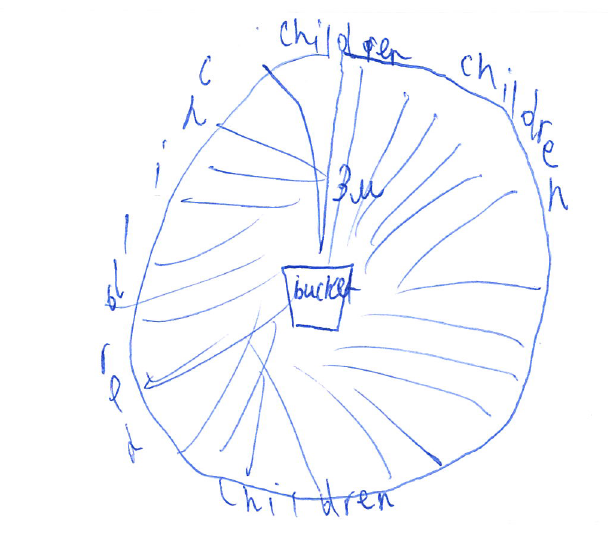
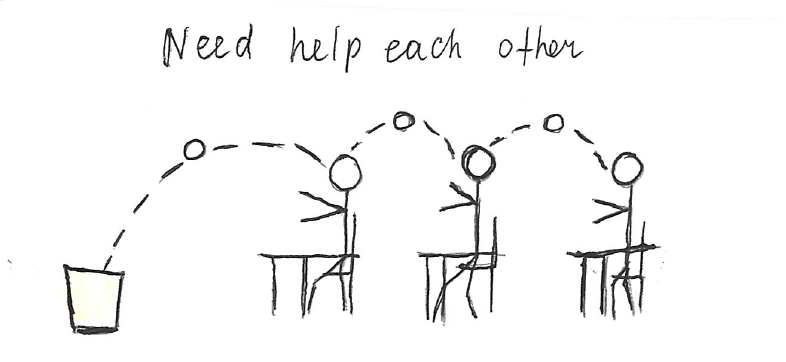
Privilege is like an invisible door. You can walk right through it and never realize it's there until it shuts close for somebody else. y grandmother never went to school past the age of ten. She's a little too loud and boisterous at times, is never afraid to speak her mind, and to my family's embarrassment, can always be found haggling shamelessly with local shopkeepers to maximize savings. To some, her behavior may appear crude, but to me, my grandmother exemplifies the kind of rare and selfless individual who gives so much of herself away to help others that she's perfectly content with just being happy that others experienced success from her sacrifices. Grandmother never went to school past the age of ten. Being the eldest of three children, she stayed home full-time to look after her younger siblings. Born and raised in a time and place where getting an education was considered a luxury, my grandmother never had the chance at a post-secondary education, but I did. I am afforded so many more opportunities because of the country of my birth and the situation of my upbringing. It took me a while to realize it, but the success I've experienced in my life was as much pure luck as it was hard work. I was born into a privilege that my grandmother did not have and I have the chance to do something about it. Inspired by my grandmother, I adopted a simple classroom activity about privilege from an article I found here. I remember talking excitedly with a friend about this activity and the powerful messages it sends about the concepts of privilege, equity, and equality. I was not a teacher yet, but I was keen to start building the foundations for a classroom environment structured around social justice. My friend considered this for a moment, then said to me, "It's a great exercise. But the problem with these types of activities is that it can't just be about awareness. Okay, so we all have privilege to varying degrees, some more than others - so what? The question you need to ask next is: 'Now what can we do about it?'" I took her suggestion to heart and asked my students exactly that. With some help from a colleague, here is the follow-up activity I presented to my students: 1. Draw it- draw a picture to show what you would do to solve this problem. 2. Share it- share your solution with three other students in the class. 3. Write it- Now that you've listened to others' solutions, write down a few sentences to add to your solution. Despite the language barrier, my students surprised me with their many insightful responses. See their work below: Instead of sitting in rows, we should aim for a more optimal arrangement. Even better, perhaps we should all be equidistant from the bin. Sometimes, we need a little help from each other. Or maybe each person should be given multiple chances. Or what if... we each had our own bins?
0 Comments
Lesson Theme: Introduction to Probability and Counting Prerequisite Knowledge: Permutations and Combinations Here's an activity that I introduced to four groups of tenth graders in a recent unit on probability:
Provide minimal guidance as the groups decide on the number of combinations for each scenario. I made an exception for students who asked clarifying questions, such as: - Are there any repeating digits? - How many digits repeat? The hints are open to interpretation on purpose in order to get students thinking about the sorts of constraints they would need to consider when calculating the total number of outcomes. The discussion phase of the activity provided a rich opportunity to address student misconceptions about permutations and combinations, as well as the importance of reasoning, i.e. Does this number make sense? Is this estimate too high or too low? How does this number compare with my initial guess (intuition)? What if there were no constraints, what would the answer be? The Solutions: TEAM GARRY - 3 digit code, repetitions allowed. This hint is not much of a hint at all. "Repetitions allowed" could mean that there may be or may not be any repetitions in the code. So, one possible answer is simply 10 x 10 x 10 = 1000. There are ten ways of picking the first, second, and third digits. TEAM ORVILLE - 3 digit code, no repetitions. This narrows the playing field a bit. 10 x 9 x 8 = 720. Ten ways to pick the first digit, only 9 choices left for the second, then 8 for the third. TEAM APRIL - 4 digit code, numbers 2 and 3 appear in the code. (a) This would be significantly easier if the ONLY numbers in the code were 2 and 3. There are only 4 possible combinations, which are easy to figure out by hand: {2323, 3232, 2233, 3322} or 4!/ (2! x 2!) = 4. (b) With repetition. There are 4 ways of positioning the "2" in a four digit combination. For each way that the "2" has been positioned, there are 3 ways to position the "3." In total, we can arrange the digits "2" and "3" in 4 x 3 or 12 ways. If repetition is allowed, the total number of combinations would be 12 x 10 x 10 = 1200. (c) Without repetition. Similar to above, except that once we have found a placement for the "2" and "3", there are only 8 and 7 digits left to choose from respectively. The final answer would be 2 x 8 x 7 = 672 My notes and observations:
|
April SooInternational math educator who writes, occasionally. Archives
April 2020
Categories
All
|








 RSS Feed
RSS Feed
