|
Hello and thank you for visiting my site! I've migrated my content to a new domain, check it out!
www.aprilsoo.com
0 Comments
We asked 101 high schoolers the following question: There are 125 sheep in a flock and 25 dogs. The question is an invitation to take a closer look at the kinds of mathematics that we are asking students to engage with in our maths classrooms today. What does it mean for us as educators when students give responses like 130 because 125 + 5 = 130 or 25 because 125/5 = 25? Moreover, what does it mean for us as educators when we expect these responses from students? I first heard about the shepherd question through Robert Kaplinsky though the question has its origins based on research by Professor Kurt Reusser from 1986, possibly sooner. ContextThe data was collected via an online survey (on account of school closures due to COVID-19) and was given to students in China earlier this year. Our initial goals were:
Results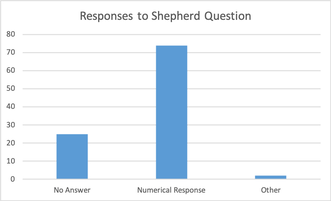 Of the 101 student who were surveyed:
At first, this data seems to be consistent with the results from Kaplinsky's experiment with the 32 eight graders, in which 75% of them gave numerical responses by using random addition, subtraction, division, or multiplication of 125 and 5. Upon closer examination, however, we see that of the 73 that gave numeric responses, 28 used random math procedures, thus not making sense of the problem, but 45 of those students gave some sort of reasoning independent of the problem to support their numeric responses. Sample ResponsesStudents that gave numeric responses by combining 125 and 5 via random math operations (not making sense): Note that a couple of students pointed out that there seemed to be an issue with the problem, but proceeded to give an answer anyway. Students that did not provide a numeric response (making sense): One response in particular really blew me away (click to expand the image): Not only did this student state that the question did not give enough information to provide a specific answer, they used what information was presented in the problem, along with sources to support their thinking, to deduce an age range for the shepherd! Wow. How can I get the rest of my students here?? This is the point where I began to see another category emerge... Students who provided a numeric response, but justified their answers outside the range of expected range numeric responses such as:
ResultsMy Take-AwaysI was quite blown away by the number of students that treated this as a "trick" question and thus gave a wide range of responses, which ranged in creativity and depth of thinking. Like I mentioned, I found it difficult categorizing some of these responses, and found that after reading that Superstar response from above, my expectations rose (not necessarily a bad thing, but definitely made categorizing more difficult).
Some factors worth considering:
It is also worth noting that in a follow-up reflection activity with students, some pointed out the need for teachers to ask less ambiguous problems, a few attributed their responses to poor understanding of the problem due to language barriers, while a fair number mentioned the importance of practicing different kinds of problem solving to develop critical thinking skills. This, I think, is a step in the right direction. Teachers are getting a bad rap these days. To put it in perspective, my own mother -- to whom I am and shall always remain eternally grateful for -- expressed her annoyance at the fact that Ontario teachers were, yet again, going on strike. (I will also add here that she is also very supportive of the fact that her own daughter chose teaching as a profession). Like others, she felt that the strikes are an unnecessary waste of time, making teachers appear selfish and lazy. When asked what information she had to support her claim, the figure "100K" came up in conversation. WHAT? How much are teachers making a year? $100 000. One hundred THOUSAND Canadian dollars. The supposed "average" salary Ontario teachers make a year. Reported source? "The government." Had it not been for the fact that a) my mother has a tendency to exaggerate the truth and b) I am a teacher myself, I may have been inclined to side with her claim. To add a bit of context: I have been teaching for five years internationally and making nowhere near that figure. For me to be earning 100K a year, I would need to have my masters degree and an additional fifteen years of full time experience. Let's Talk About Averages "Average" is a misleading term; it can refer to the mean, median or mode. In statistics, we call these "measures of central tendency." Let me borrow an example from Wheelan's book (Naked Statistics) to make a point. Suppose five people are at a bar, each earning a salary of $35k a year. Undisputedly, the average salary (by all counts) of the group would be $35k. Typically, when we hear the word average, we equate it with the mean, which is the sum of all the points in a data set, and divided by the total number of values within the set. Suppose Bill Gates walks into the bar, with a salary of $1 billion a year, bringing the average (mean) salary to $160 million. The reported figure, while still accurate, is not a fair representation of the average earnings of the majority of individuals in the group. In this case, the knowing the median (middle value when all values are arranged from smallest to greatest) provides a bit of context. After all, the difference between 35 thousand and 160 million is no small sum. This is a classic example of how precision can mask accuracy. Think about any time you've heard a number or figure reported in the news, consider the following statements, for instance: Statement 1: "99% of statistics are made up" (Ha!) Statement 2: "I have here in my hand a list of 205 -- a list of names that were made known to the Secretary of State as being members of the Communist Party and who nevertheless are still working and shaping policy in the State Department" - Joseph McCarthy, a US previous senator (1950) Don't these it seem to bring credibility to whatever claim the person or organization is trying to assert? The first statement is, of course, made up. As for the second statement, it turns out that the paper had no names on it at all. Statistics is a tool that helps us bring meaning to data, but can be abused for nefarious purposes if wielded irresponsibly. We should be cautious While math may be infallible, we are not. No matter how convincing the data may be, there is always more than one way to interpret it. It's a little like telling your friends and family that the guy you just met "has a great personality," which almost always implies that there is some other flaw or red flag that has not been said (Wheelan 37). So, back to the this 100k salary I'm supposed to be making... How did they get this data? What are the demographics of the teachers being surveyed? (It makes a difference if the majority of teachers who have been working full time in Ontario have at least 15 years of experience under their belt). Are they including retired teachers? Teachers who have recently been laid off? I tried to trace the origins of where this figure of 100k came from. After a bit of digging, I think its likely that my mother mis-reported the figure she heard from sources that gave out misinformation. [NOTE FROM THE AUTHOR: I purchased Naked Statistics by Charles Wheelan many years ago, thinking its an important book to add to any Math Teacher’s arsenal (and it is!) but had only gotten through the first three chapters before dismissing it for another read. It is not a boring book - quite the opposite in fact - but I felt that mere passive reading was not enough for me to really retain the important ideas and intuition that Wheelan is trying to impart to his readers. This time, I’m giving it another chance and plan to summarize material I am learning, relate it to my own experiences, and share that learning here on my blog.] Shortly before the start of our Chinese New Year holiday at the end of January, news had started to spread about a new virus in Wuhan, China. By the time I actually left the country, virtually everyone was wearing a face mask and activity at all major transportation hubs (railway stations, airports) had basically stalled. For a while, it seemed like we were able to escape the mass hysteria that was beginning to ensue and enjoy nearly three weeks of worry-free traveling around the Philippines. My travel companion, Jose, and I had been keeping a close tab on the coronavirus situation, and we were warned by my relatives in Hong Kong to stock up on as many face masks and hand sanitizers as we could while we were in the Philippines as they were virtually sold out everywhere in Hong Kong and China. We had originally planned to return to Shanghai on February 16th but had been notified by our principal that the start of physical classes in China had been delayed until at least March 2. At that point, the number of reported infected people had been raising still and we contemplated travelling elsewhere to ride out the situation. The problem was, we had, and still have, no idea how long this situation would last, nor have we been given any sort of certainty as to a specific return date for work. Jose ended up returning to Suzhou, where we both work and undergoing a 14 day quarantine, which was monitored by the building management. I made a last minute decision to return to Canada. Both our decisions were spurred on by an unfortunate encounter with bed bugs (we suspect), and us having to deal with two very different sets of symptoms that caused us a lot of emotional stress and worry. Luckily for us, we're on the path to recovery. As far as I know, majority of international teaching staff from our school are taking "extended vacations" (using this term loosely here) in various countries around the world. A few have opted to go back to Canada, some returned to China, and a few never left.
I know that many teachers and schools express issues with using WeChat as a way to communicate with students, and this was something I had a lot of hesitations with as well, which is why I've never created WeChat groups for my classes in the past. Over my last few years though, I've quickly realized that it is really the best and fastest way to reach students, and I've joined and created WeChat groups for sharing or keeping up to date with school-wide announcements, communicate with course teams or departments in the school, or get in touch with students who are part of extracurriculars I'm running. WeChat is not just a messaging app, but also has social media features, payment options, and several other utilities built in. In short, WeChat is pretty much woven into the fabric and lifeblood of what living and working in China is like. That said, it is THE number one tool to utilize if you are looking for a stable and reliable method of communicating with people in China. No server issues, no need for a VPN… so while privacy is still a concern, it is now a part of my online instructional plan. (There is an option to limit communications with contacts to "chats" only so you can hide your social media posts). Moodle is, and remains, the MAIN communication platform for students to access course materials, view links to filmed live sessions, submit assignments…. And so on. A couple of other tools that my colleagues have introduced that I've found extremely helpful for my classes include Zoom, an online conferencing tool, and Loom, a video recording software that uploads any videos you make onto a cloud and sharing a video is as simple as copying and pasting a link.
Given that we've been fully online with our learning for about two weeks now, we're addressing minor hiccups as we go, adjusting the pacing of our lessons, and working on finding authentic ways to assess student learning. We're thinking about how to troubleshoot potential issues with academic honesty and ways to get an accurate and holistic picture of how our students are learning. The biggest unknown at the moment is when we will be back in the classroom, and how the coronavirus situation will pan out… Guess we'll just have to wait and see. We've been looking at map projections for my masters course and I continue to be blown away by how embedded mathematics truly is in our every day lives. As a self-identified directionally-challenged individual, geography and anything like it is to be avoided at all costs. I find myself at my wit's end now and have to admit that even maps hold a lot of mathematically intriguing ideas that are worth exploring. The course I'm taking now is called "Math for Global Citizens", offered at the University of Waterloo to MMT students, taught by Judith Koeller and is arguably one of my favourites in the program. The problem of the "flat earth" has been around for centuries. It is believed that as early as the year 354, pre-medieval scholars asserted that the earth was in fact spherical (University of Waterloo). The problem for map-makers, then, is to find a way to depict a spherical object on a 2D surface, and this is turns out to be an impossible task. Take a look at the animation below for what's called a "Myriahedral projection" developed by Jack Van Wijk from the Netherlands. The idea behind a "Myriahedral projection" is to split the earth up into polygons, thousands of them, in order to preserve both shape and size of major land masses or bodies of waters (see article here). Map projections have not always been so advanced however. In trying to depict a spherical surface onto a 2D plane, one can try to preserve distances, shape, areas, or shortest distances between points by straight lines. It is impossible to have all these desirable properties in one map. For instance, the Mercator projection map is the one that we are probably all most familiar with as it preserves angular distances, making it easy for navigation, but it drastically skews areas the further away the land masses are from the equator. See this true size (thetruesize.com) comparison below, showing how large the continent of Africa actually is compared to the US, China and India: On that note, I would highly recommend checking out thetruesize.com and just playing around. Here's another great video explaining "Why all world maps are wrong" that was recommended to me by Mr. Schwartz, a geography teacher and the humanities Department Head at my school. What is the point? The point is to do math, or to dazzle friends and colleagues with advanced statistical techniques. The point is to learn things that inform our lives. - Charles Wheelan [PREFACE: I purchased Naked Statistics by Charles Wheelan many years ago, thinking its an important book to add to any Math Teacher’s arsenal (and it is!) but had only gotten through the first three chapters before dismissing it for another read. It is not a boring book - quite the opposite in fact - but I felt that mere passive reading was not enough for me to really retain the important ideas and intuition that Wheelan is trying to impart to his readers. This time, I’m giving it another chance and plan to summarize material I am learning, relate it to my own experiences, and share that learning here on my blog.] I wrote about why statistics matters in a previous post. Here, I continue to elaborate on the point as I summarize my biggest takeaways from the first chapter. This chapter provided an overview of big ideas in statistics that we’ll be learning about throughout the book. Description and Comparison Descriptive statistics is like creating a zip file, it takes a large amount of information and compresses it into a single figure. This figure can be informative and yet completely striped of any nuance. Like any statistical tool, one must be careful of how and when we employ such figures and the implications it might have on the audience. So a descriptive statistic is a summary statistic. Let’s start with one that many of you may already be familiar with - GPA. Let’s say a student graduates from university with a GPA of 3.9. What can we make of this? Well, we might be able to discern that on a scale from 0 - 4.0 a GPA of 3.9 is pretty darn high. But some universities grade on a scale of 0 - 4.3, accounting for a grade of A+. What this simple statistic doesn’t tell us is what program did the student graduate from? Which school did they attend? Did they take courses that were relatively easy or difficult? How does this grade compare with others in the same program? Wheelan writes, “Descriptive statistics exist to simplify, which implies some loss of nuance or detail (6).” Inference We can use statistics to draw conclusions about the “unknown world” from the “known world.” More on that later. Assessing Risk and Other Probability Related Events Examples here include using probability to predict stock market changes, car crashes or house fires (think insurance companies), or catch cheating in standardized tests. Identifying Important Relationships Wheelan describes the work of identifying important relationships as “Statistical Detective Work” which is as much an art as it is a science. That is, two statisticians may look at the same data set and draw different conclusions from it. Let’s say you were asked to determine whether or not smoking causes cancer? How would you do it? Ethically speaking, running controlled experiments on people may prove unfeasible, for obvious reasons. An example Wheelan offers here goes something like this: Let’s say you decide to take a few shortcuts and rather than expending time and energy into looking for a random sample, you survey the people at your 20th high school reunion and look at cancer rates of those who have smoked since graduation. The problem is that there may be other factors distinguishing smokers and nonsmokers other than smoking behaviour. For example, smokers may tend to have other habits like drinking or eating poorly that affect their health. Smokers who are ill from cancer are less likely to show up at high school reunions. Thus, the conclusions you draw from such a data set may not be adequate to properly answer your question. In short, statistics offers a way to bring meaning to raw data (or information). More specifically, it can also help with the following:
Lies, damned lies, and statistics. - Mark Twain
It’s easy to lie with statistics, but it’s hard to tell the truth without them.  [PREFACE: I purchased Naked Statistics by Charles Wheelan many years ago, thinking its an important book to add to any Math Teacher’s arsenal (and it is!) but had only gotten through the first three chapters before dismissing it for another read. It is not a boring book - quite the opposite in fact - but I felt that mere passive reading was not enough for me to really retain the important ideas and intuition that Wheelan is trying to impart to his readers. This time, I’m giving it another chance and plan to summarize material I am learning, relate it to my own experiences, and share that learning here on my blog.] A couple of days ago, my younger brother, who just started his first year in university in the Fall, was complaining to me about the woes of student life; in particular, the obsession with grades and the paradoxical lack of willpower to work for them. Having taken an accounting class together, his friend recounted to him that it was, “The sketchiest 90 I ever received.” Let’s break that down for a moment. Humble brag? Yes, but what he really meant was that his friend was blindly memorizing formulas, plugging and chugging without any idea how they were derived and why they are meaningful. Does that sound familiar? How many of you have had similar experiences in math class? I know I have. Not just math, but in science, language arts, history… sometimes it feels like we are just memorizing facts in isolation without an understanding of their greater purpose. To be fair, I’ve taken statistics classes that feel no different, a series of formulas that need to be applied to raw data. What makes statistics inherently different, however, is that unlike calculus or algebra courses, which often teach skills in isolation of their applications (to which I will argue there is intrinsic value in knowing and learning, another post perhaps) statistics IS applied mathematics. Every formula, number, distribution test...etc. is meant to clarify and add meaning to everyday phenomena (though, when wielded improperly, can have the opposite effect). Statistics are everywhere - from which are the most influential YouTubers, to presidential polling to free throw percentages. What I love about this book is that it focuses on building intuition and making statistics accessible to the everyday reader. A quote by Andrejs Dunkels shared by the author, “It’s easy to lie with statistics, but it’s hard to tell the truth without them.”  This blog post is about how the math department at my school in Suzhou, China implemented changes to the way we taught Math 10 and 11 to incorporate data and research from cognitive science to help our students learn better. I include a summary of what we learned, and some ideas for improvement. It began last summer, at math camp. Yes, I attended math camp as a fully-fledged adult! Yes, there were other adults present. And yes, it was awesome! (Officially named the “Summer Math Conference for Teachers” but let’s not get into the nitty gritty). One of my favourite sessions was the one led by Sheri Hill, Arian Rawle, and Lindsay Kueh on the grade 10 course redesign they have implemented in at their school in Ontario. The course redesign is based on research and best pedagogical practices outlined in the book Make It Stick, The Science of Successful Learning by Peter C. Brown, Henry L. Roediger III, and Mark A. McDaniel. Book Synopsis: Why is it that students seem to understand what is being taught in class but end up failing when it comes to test day? How does one progress from fluency to mastery over challenging content? Many common study habits like re-reading and highlighting text create illusions of mastery but are in fact completely ineffective. This books explores insights from research in cognitive science on learning, memory, and the brain, as well its implications on teaching and learning. THE WHATAfter the session, I couldn’t wait to bring these ideas back to the math team at my school in Suzhou, China so we could start putting them in action too! We began by looking at issues we noticed our students faced:
We made it our goal to address some of the issues above, taking many ideas directly from the session presented by Hill, Rawle, and Kueh. Like Hill, Rawl, and Kueh, we removed unit tests, which freed up a significant amount time for other topics and activities. Instead, we moved to weekly cumulative quizzes that held students accountable to everything they have learned in class up to the Friday before quiz day (no skills expire!). The weekly schedule looks as follows:
|
|||||||||||||||||||||||||||||||||||||||||
| Sample Fast Fours | |
| File Size: | 38 kb |
| File Type: | |
| Sample Weekly Quiz | |
| File Size: | 891 kb |
| File Type: | |
I had lofty plans. I'd been refreshing myself on Jo Boaler's work about mathematical mindsets (see my previous ramblings here). I was going to do a little study. Please note that I do not have any experience whatsoever doing educational research. While I have a general understanding of the scientific method, I was mostly doing this out of pure curiosity and a desire to become a better teacher.
Like all good mathematicians and in the name of good science, it was perhaps inevitable that first time was not the charm, and rather than have a very successful, replicable study, I instead gained some knowledge about how I might proceed in the future. Nice.
Content that I had planned to cover in 10 days would have taken closer to 18. The students had an incredible range of English speaking ability, with drastically varied dynamics between groups of students. The schedule did not operate on a cycle, so I saw the same group of students at the same time each day, which definitely influenced their learning experience. For instance, Group C who were absolute angels and ready to learn each day in my first period class were exhausted by the time they got to third period, which led to more behavioural problems in the classroom.
STUDENT DYNAMICS
Group A: A challenging group. I saw them the period right before lunch each day and there was a group of four students who were unable to sit still and wandered the class during inappropriate times, such as in the middle of me giving instructions. I lost my cool on this group; shame on me because I wasn't able to regulate my emotions and respond calmly to the situation. Just to clarify, a "losing my cool" moment for me doesn't mean shouting or yelling, which is neither helpful nor productive. I simply raised my voice to get the students attention. But, in that moment, I had lost my cool because I let the students dictate my response rather than carefully assess the situation and respond calmly and accordingly.
Group B: Did absolutely anything in their power to NOT pay attention. Would whine anytime I introduced a new activity. Would put their heads down and sleep in class. I saw this group after lunch each day, they were my last and perhaps most challenging class because of the incredible amount of sleepers and students who wanted to do absolutely nothing. There were definitely some gems in this class that would have benefitted from being in a group with other, more responsive students. Lots of patience and flexible teaching strategies required.
Group C: The first group I saw each day and by far the best group. Students had a decent command of English and I rarely had to repeat myself. They would listen and follow instructions the first time. Students would always do as they were asked. The challenge with this group was pushing them to work slightly beyond their zone of proximal development.
Group D: A diverse group with students who always wanted to be two steps ahead, students who needed a lot of personal assistance, students who got distracted easily, and students who were happy with just coasting along.
HOW I COLLECTED DATA
I used Boaler's Mathematical Mindset Teaching Guide as a self assessment tool for how I was and was not strengthening growth mindset culture in my math classroom. I wanted to focus on changing students' inclinations towards math learning, challenging those who believe math is a subject that defies creativity and passion, and pushing those who already saw themselves as "math" students to expand their definition of what math is. With the help of my math mentor, I settled on collecting data through a mindset survey.
Students took a before and after survey. I added two prompts on the after survey that required students to provide written answers to the following:
- What I think math is...
- How math class makes me feel...
A source of error here is that for students with low English level, they may not have fully understood the meaning of the statements they were agreeing or disagreeing with. Another possible source of error (though unavoidable) are those students who "did" the survey by randomly clicking boxes just to appease their dear teacher.
HOW I TAUGHT
I chose content from YouCubed's Week of Inspirational Math. I chose these tasks because they were all low-floor, high-ceiling tasks and were designed to build good mathematical habits of mind. For example, on day 1, we did an activity called "Four 4's" which encouraged students to think creatively and work collaboratively to come up with as many expressions as they can that equal the numbers 1 - 20 using only four 4's and any mathematical operation of their choice (see picture below).
Other activities we did:
- Escape Room Challenge: A mixture of math puzzles, grade 9/10 content from trigonometry, polynomials, and simplifying expressions. Designed by me and was meant to last one period, ended up taking two.
- Number Visuals: Students examined visual representations of numbers 1 - 36 and were asked to identify and describe patterns (prime v composite numbers, factorization...etc.).
- Paper Folding: An activity from YouCubed that challenges students to slow down and justify their answers. (Meaning that, anybody who claimed they were "finished" after five minutes clearly did not understand the activity...)
- Movie: Students complete an agree/disagree questionnaire and watched The Man Who Knew Infinity about an Indian mathematician named S. Ramanujan making waves in England. Great movie starring Dev Patel. We did a discussion circle afterwards that touched base on prompts from the questionnaire that students were interested in exploring. (E.g. "Math is creative")
- Pascal's Triangle: Find and describe patterns hidden in Pascal's triangle.
In terms of assessment, I wanted to stay as far away from tests or quizzes as possible. Instead, I focused on providing students with specific, written feedback on their journal entries, group quizzes, and one final presentation at the end. I wasn't concerned so much with what they knew, but rather the process through which they were learning and engaging with the material.
Before | After |
"Interesting"
"The most important things we need to learn"
-"Have unlimited creativity"
"Magic"
"Subject between creative and and teamwork"
"is very interesting. make my brain growing"
"beautiful"
"fantastic"
"Math makes me hate and love"
Select responses to "How math class makes me feel"
"Better"
"Moer interesting than chinese class"
"It may not very interesting, but OK"
"happy that I learned a lot"
"I feel very good, I meet very good teacher also know the very good friend in the math class"
"exciting"
"I feel happy when I fiand the ancer"
"free"
"Good! make me more confedent"
WHAT I LEARNED
A majority of students already had tendencies towards a growth mindset in mathematics, perhaps as a result of the general high regard Chinese people hold for mathematics as a subject. For the most part, students liked math and saw themselves as capable of achieving if they worked hard enough. Of the 59 students I taught, a small number of students (three or four) were of the opinion that they were "just not math people" and were extremely hesitant in trying.
In the end, I can't really say definitively which factors of my teaching influenced (or failed to influence) a stronger growth mindset towards maths. What I do know is that the switch to low-floor, high-ceiling tasks was extremely freeing -- for me and for the students. It allowed us to take a concept or idea as far as we wanted to go. There was no script or prescribed problem set that the students had to work through in increasing levels of difficulty, but rather a greater depth of thinking, and the time and space for that thinking to happen. Despite (or maybe thanks to?) the lack of testing (there were none), students still engaged with the tasks and content at high levels, drawing conclusions they might never have done with a pre-made worksheet of the skills they were supposed to practice.
By building a stronger focus on increased depth of knowledge, it then follows that a necessary norm to advocate would be that math isn't about speed. When people refer to themselves as not "math people", that's usually what they refer to, the fact that they aren't fast at mental arithmetic. But math is so much more than that.
In all, while it is hard to say from the students' perspective whether or not they appreciated a stronger switch to teaching with mathematical mindsets in mind, I know that for me it resonates as a noble endeavour. Yes, it is much easier to write a test and spend 70 minutes of your life making sure no one cheats. But take that same test, rip it up, and replace it with a diagram, an equation, a single question, a blank sheet... and possibilities begin to emerge. Some groups may reach a higher level of understanding and some may not, but then again, we teach students, not subjects.
Two weeks later, I ran an escape room in my classroom. It was the most fun I'd had all year.
Cue intro. Goal: Answer the question, "what is life?" Other than that, I gave my students VERY little prompting. I figure I'd let all the mysterious new locks that had been placed in my classroom do most of the talking.
Clue 1: Integration
Students were given a numeric code that had to be converted to a word after correctly solving the given integration problem.
The answer was "SNACKS," which happens to be a location clue, leading to the refreshments centre where I provide students with water, tea, and snacks. The answer to the first clue was hidden under the snack basket. Many students got stumped at this point and wasn't sure what they were supposed to do (I didn't give them ANY other instructions). Once they got going, however, they really got into the flow of it.
I used a matching activity here from Flamingo Math (teachers pay teachers) and students had to find the four digit number code based on the highlighted boxes. (So they didn't actually have to complete the entire matching activity).
The answer: Students convert correct answer into letter code to unlock the letter lock.
Clue 4: Calculus Crossword
The answer: Highlighted in invisible ink are the words TRIAL.
- DON'T set letter locks to be something obviously related to your subject. I stupidly set mine to be "MATH" and had students guessing random four letter words rather than actually engaging with the problem sets that I had worked so hard to create! (I later changed the combo to "BATH")
- On that same vein, you can set a rule so that students can only attempt one combination at a time.
- There's always that one kid who examines everything with the UV light... so I ended up writing a few random messages around the class not related to anything but just for giggles.
A great format for STEM OLYMPICS
ROUND 1: Unlock one of three boxes
- Event began with nine teams of four
- Students work in teams of four, they have a choice of which question set they would like to work on, however, once a box gets unlocked, then that box becomes unavailable
- The question sets corresponding to each box cover a different range of subjects (ex. Box A might cover Math 10, Science 10, Physics 11 and Chemistry 11 while Box B might cover IT 10, Math 10, Science 10 and Math 11).
- Inside each box are a series of "advantage cards"
- Only the teams that unlock the boxes proceed to the next stage of competition
ROUND 2: Gain 5 points in a trivia style tournament
- Each box contained a specialized advantage card that can be used in round 2
- Advantage cards may only be played after the question topic is revealed and BEFORE the question is revealed
- Examples of advantage cards: skip the question, make the question worth double points, invite an expert to answer the question
- First team to 5 points wins
- Remaining teams compete for second place

Since then, I've created two other escape activities with my classes. They're a lot of fun to make and the possibilities for clues and questions are endless! This is definitely an activity I'm going to keep using in my classes.
In all honesty, when I graduated teacher’s college, I panicked. Having been a part of the concurrent education program at Queen’s University, I was in a class full of driven and hard-working individuals who always had a plan. Everybody in the program (or so it seemed) knew they wanted to teach, and they pursued that goal relentlessly. By the time February rolled around, a lot of people had already gotten offers or had jobs waiting for them. By the time I graduated, I had nothing.
Knowing what I know now, finding yourself jobless after graduation is completely normal. What felt like weeks of unemployment was actually mere days. What seemed like dozens of personalized cover letters and job applications was probably more like five or six. In fact, it took me about two weeks to get a job. I wasn't picky, knew I wanted to be overseas and it didn’t matter where. So when the opportunity presented itself to teach in Kazakhstan, I went for it. One job interview later, and I was preparing myself for life abroad.
I only stayed in Kazakhstan for a year. The contract itself was a dream (great pay, light workload), but my gut told me it wasn’t the right job for me. When I decided I wouldn't return for a second year, many experienced teachers cautioned me I would never find another job with the same benefits and salary, and they’re probably right. But I left. Eventually I ended up in Korea. Long story short, a very different experience from Kazakhstan! The work hours were longer, the work was more taxing at fraction of the pay, in a city whose standards of living were much higher, but it felt more real.
Eventually, I left Korea too. That’s a whole other story. Now I’m in China… a place I never thought I’d end up working. A place I never had any desire to work in. I just felt like too much of an anomaly – “Who is this girl that looks Chinese but cannot speak the language and behaves differently from us?”
When I think about my experiences growing up as a Chinese-Canadian, I carry a lot of guilt and shame. It feels like there is this great burden to fit in and be accepted into different social groups, but also pressure to live up to your family’s expectations and pass on the culture, traditions, and language to the next generation. If I leaned too much to the left, I was too jook sing (roughly translated as “kid who betrays one’s cultural roots”), and if I leaned too much to the right I was considered too much of a FOB (“fresh off the boat”). Rather than living up to my cultural/familial expectations (whether spoken or implied), I tried to run away from them. I decided that being an outlander in a country where I am very clearly foreign would quench those weird notions that I had about fitting in once and for all. I would work anywhere but China, I decided. Oh the irony.
I’m happy to report that these feelings of guilt and shame have mostly subsided, or at least, I have come to a peaceful cohabitation agreement with them. In fact, being in China has helped me feel more connected to my culture and my family. I’m even taking Chinese classes again! For me, that is a big frickin’ deal, and this time, a step in the direction I want to take.
One of the course modules talks about creating or giving students tasks with a growth mindset framework, which has the following components:
1. Openness
2. Different ways of seeing
3. Multiple entry points
4. Multiple paths/strategies
5. Clear learning goals and opportunities for feedback
The example that is given from the course is as follows:
A teacher might ask, "There are more squares in case 2 than in 1, where are they? There are more squares in case 3 than in 2, where are they? Describe what you see."
Go ahead and try this task on your own first. Watch the video to see examples of different responses (skip to 3:50).
I decided to try a similar task with my Pre-Calculus students in China, and picked a pattern from Fawn Nyugen's site visualpatterns.org
Here are some answers that students came up with (I posted 6 copies of the same image and challenged my classes to fill all 6 with different representations).
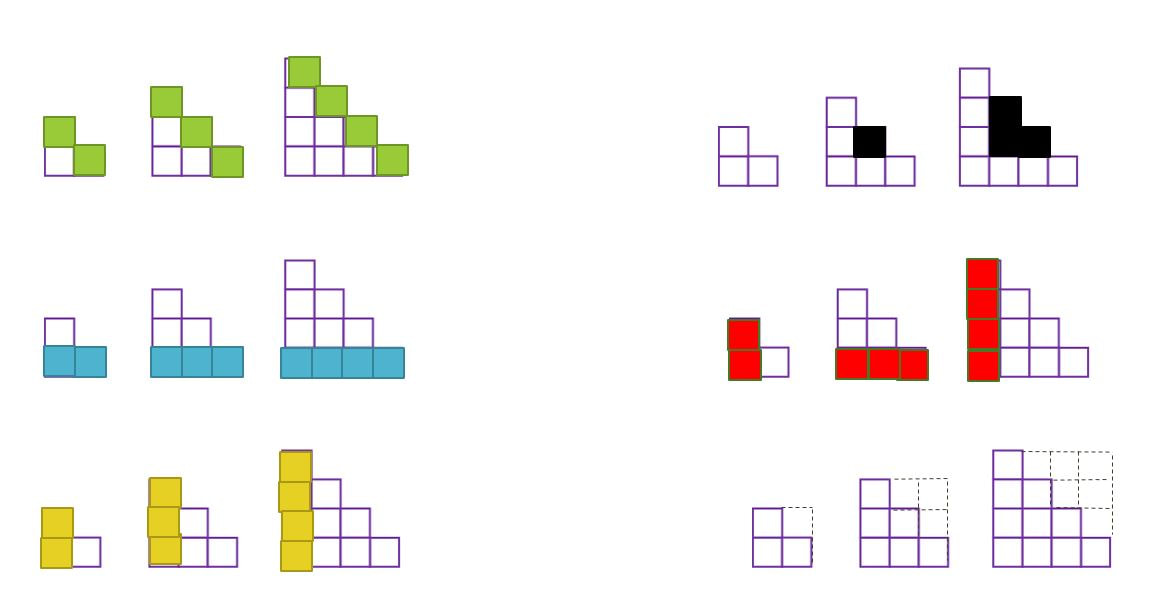
Most students were able to set up a table and saw that the difference from one case to the next increased by 1 each time:
Another student used the "square" representation as a part of his proof but isolated the last row.
Looking at the diagram below, we see that the total number of squares can be represented by (n+1)^2.
Ignoring the last row, we see that the number of actual squares and "negative space" squares are equal. The total number of squares (excluding the bottom row) is therefore given by [(n)(n+1)]/2.
Putting both these parts together, we get that the total number of squares for case n is:
-Take the square representation, ADD another layer
-Now we have a rectangle with equal amounts of actual squares and "negative space" squares
-The resulting formula is just the area of the rectangle divided by 2
- A door sign with the teacher's name, room number, and teaching schedule
-Stickers, 'cuz duh
-Coffee, a key element in sustaining the life force of a teacher
-A pack of cards, essential in any math teacher starter kit
-A math puzzle, fuel for the brain
I'm super happy with the way they turned out, and I'm looking forward to a good year ahead!
I've added some modifications and created an accompanying PPT that's a full lesson, all ready to go. Scroll down below to access this resource :) I'm a big believer in sharing teaching resources for free, and this is my way of giving back to the online teaching community that has given so much to me. Huge shout out to everyone in the #MTBoS, I love this community.
The activity works as follows:
1.Students it with a partner, shoulder to shoulder.
2.One person faces the board, the other person faces away.
3.The person facing the board will be the explainer.
4.The person facing away will be the grapher.
Warm Up: Teacher does warm up round with the students, describing a basic graph (ex. linear function) and students attempt to draw it in their notebooks. Discuss: What prompts were useful? Is there something the teacher said that could have made it easier?
The Activity: (see above)
Exit Ticket: Given a picture of a graph, students are to write a description that matches it in as much detail as possible.
Extension: Students draw a graph and write a corresponding description. Scramble the results and have students match them!
| grapher-explainer_activity.pptx | |
| File Size: | 2261 kb |
| File Type: | pptx |
<3
Day 4 - Ancient Cities in Mandalay
For our first stop, our driver took us to a monastery in Mandalay where we had the opportunity to speak to his friend, a monk who teaches English there. We were shown around to various buildings (the dormitories, dining hall, study halls...etc.) and learned about life in the monastery. Becoming a monk is a well-respected and esteemed route to take for boys and men of all ages. A family's status is elevated if they have a son who decides to become a monk. Of course, not many choose to stay one, some quit years, months, weeks, or even days into monkhood, which is not uncommon. At one point, both our taxi driver and tour guide (whom we would meet later in Bagan) had taken up monastic life.
At the monastery, we met an especially charming and charismatic young monk who went by the name of "Drake." Funnily enough, we would later run into "Drake" again three days later in a totally different city, at sunset, on the top of a temple, where he would re-introduce himself as "Maha Raja," and add us as Facebook friends. To this day I am still not sure if he is using his real name.
Like Mandalay Hill, U-Bein bridge is a popular tourist destination at night time, as people like to go for the sunset. We decided to go earlier in the day to avoid the crowd. Here, we purchased some coconut ice cream (DELICIOUS) and walked about halfway across the bridge before turning back... on account of some uncomfortable cat calling. We weren't dressed in scantily clad clothing by ANY means but my Sarah does happen to have strikingly blonde hair and fair skin which drew a lot of unwanted attention. We definitely had to check our privilege at that point.
PRO-TIP #1: Please don't do what we did and walk the entire length of the bridge! We missed out on exploring Amurapura city as a result, but we ended up having a great day regardless (read on to find out!)
The next part of our journey would be my favorite in Mandalay. That was our brief tour of the ancient city of Inwa.
PRO-TIP #2: Keep in mind most places you visit will require you to go barefoot (temples, pagodas, ruin sites...etc.), so bring comfortable shoes that slip on and off easily!
On the way back, we saw a little boy and a dog at one of the ancient ruin sites.
But still, it was a fine friendship.
We decided to explore the area.
And so we did.
And saw the most breathtaking statue.
There was something about the way the light fell, the little boy giggling and running around us, the other little one who turned out to be his brother, prodding us along, telling us to climb here, sit there, pose like this, not like that... Making faces at us when we did something they didn't like and giving us the thumbs up when they deemed we had the perfect pose...
What fine salesmen they turned out to be.
NEXT UP: Bagan!
Day 1 - Mandalay
Our priorities for the day: get to our hotel and get food! We exchanged what RMB we had in our wallets and took a taxi from the airport direct to our hostel, the Moon Light Hotel, which cost maybe 30 CAD (for reference, the exchange rate at the time of our travel was about 1 CAD to 1000 MMK).
For dinner, we walked to Mingalabar, the #1 rated restaurant on Trip Advisor in Mandalay, and boy - did it live up to those standards! For bout 15 CAD, we had a beer, lime soda, soup, rice, a main of lamb curry, and dessert. The main course comes with all the side dishes you see below, the idea being that you can customize each bite according to your taste preference. The side dishes they serve vary from night to night, but ours featured peanuts, fish, potatoes, cauliflower, a shrimp paste, and some raw vegetables.
A word of caution...
[For some mysterious reason, I was not able to withdraw ANY money on my UnionPay card, but luckily Sarah was able to to do on her Canadian bank card.]
Long story short, to avoid running into this issue, I would recommend bringing enough cash with you to last the trip. But beware of pickpockets, especially in touristy places!
Day 2 - Mandalay Palace
In the afternoon, we asked our hotel to help us call a taxi to take us to Mandalay Palace. If you call a taxi through your hotel, the prices are usually set (though still very reasonable). If you choose to hail your own transport, usually there is a bit more room to negotiate. Keep in mind that these are not "taxis" in the Western sense, but rather random strangers you're waving down in the streets who happen to have a car and want to make a few extra bucks driving people around.
To get into the Palace grounds, you need a visitor's pass. You'll be asked to leave your passport with the guards in exchange for one. We did not have our passports with us, but luckily, they accepted Sarah's drivers licence (phew!). In the area surrounding the palace there's a park and some temples and pagodas. We just walked around and took our time exploring the area.
Day 3 - Mandalay Hill
I can't remember what else we did in the evening (ate food somewhere definitely), but the morning hike did take up a lot of our energy. A day well spent overall.
NEXT UP: A private tour to the ancient cities in Mandalay (click here for Day 4 details.
The Challenge
It Begins with a Question…
One thing that has not changed, however, is that I avoid teaching FOIL method like the plague. It only works for expanding binomials and does not apply for polynomials with more than two terms. After I read this article I was convinced I would never need FOIL in my classroom:
http://www.makesenseofmath.com/2016/11/why-i-will-never-teach-foil.html
For a good laugh:
https://saravanderwerf.com/2017/04/01/why-ive-started-teaching-the-foil-method-again/
Some things that came up in our discussion:
- Algebra tiles - benefits and fall backs
- Picture talks
- Factoring method (criss cross or sum-product?)
- WODB
- Progress checks
- Taboo
- Human Bingo
1. Algebra Tiles
Nevertheless, we spent a few classes examining algebra tiles and their usefulness. Rather than approach it from the typical standpoint of using algebra tiles as a manipulative, I wanted students to see the link between the algebraic and pictorial representations of polynomials. This took work and was not as straightforward as it seemed. A big takeaway for me was that students gained much more out of the experience when they were able to physically manipulate the tiles and arrange them into their "factored forms." Last semester, I "taught" algebra tiles by merely showing them examples and drawing them on the board. It took a bit more prep, but this semester I printed eight sets of tiles (positive and negative) in my classroom and had students manipulate them instead.
If we were to spend any more time on the unit, or if this was a lower grade level, as an enrichment activity I would have students discuss the limitations of algebra tiles and look for ways to address them.
2. Picture Talks
What are my photo prompts, you ask?
Goals for students:
- Make observations and ask questions
- Use math vocabulary
- Share ideas with their peers
I like this activity because it is easy to differentiate and works well as a "minds on" for any topic. Asking students a general question like what they notice/wonder means that lower ability students can comment on ANY aspect of the photo (e.g. "there are blue and green rectangles") while higher ability students can be pushed towards making observations based on any mathematical patterns or relationships they observe (e.g. "the green tiles represent positive polynomials and red tiles are negative").
3. Factoring Method - Criss Cross or Sum Product?
- Common factors
- Ex: 12xy + 3x
- Ex: 12xy + 3x
- Trinomials with leading coefficient of 1
- Ex: x^2 + 4x + 4
- Ex: x^2 + 4x + 4
- Factoring when the GCF is a binomial
- Ex: x(x + 1) - 2(x + 1)
- Trinomials with leading coefficient not equal to 1
- Ex: 3x^2 + 8x + 4
- Ex: 3x^2 + 8x + 4
That, together with a quick exercise on sum/products, helped me push students towards seeing the relationship between the factored form of a trinomial, and the sum/product method.
- Focus is on noticing patterns
- Less trial and error work
- Allows them to answer questions like this:
Which One Doesn't Belong? (WODB)
Benefits:
- Everyone speaks (I always encourage full sentences and proper use of math vocabulary)
- More than one argument may arise for each expression
Sample answers:
"27x^2 doesn't belong because it is the only expression that has a coefficient with a perfect cube"
"45x^2 doesn't belong because it is the only expression that has a coefficient with 5 as one of its prime factors"
More WODB prompts can be found here.
Taboo
Modifications: Differentiate by giving students the option of bringing a "cheat sheet" of vocabulary terms with them. Prepare students for the activity by giving them cross word or fill in the blank exercise reviewing the vocabulary words for the unit. An "expert round" can include vocabulary not on the cheat sheet. "Challenge round" can be facing a peer or the teacher. Can play in teams or as a class.
Human Bingo
| chapter_5_human_bingo.docx | |
| File Size: | 87 kb |
| File Type: | docx |
Benefits:
- Gets students moving
- Students can pick the question they want to answer
- Fun review activity for a test or quiz!
This past semester I taught Math 10 and 11 of the British Columbia curriculum at an international school in Suzhou, China. With the exception of a handful of students, all of them are English Language Learners. Some might argue that this does not pose a big problem in mathematics, since the language of mathematics can be viewed as a combination of abstract signs and symbols separate from the English language. The problem is, it is one thing to understand mathematical ideas and concepts, but another to be able to communicate them. Someone who is well versed in a mathematics should theoretically be able to describe the same concept in more ways than one - numerically, algebraically, graphically, and verbally. Mathematicians strive for precision in expressing ideas, and this is not always simple. Aside from students having to approach mathematics from an ELL standpoint, the issue is compounded when you consider all the ways in which ambiguity arises in the English Language. Take for instance the word "and"; conjunction in mathematics is commutative (A^B is the same as B^A), but you can see from the example below that "and" in everyday English is not commutative.
The sentence, "John took the free kick, and the ball went into the net," would have a very different meaning if the conjuncts were reversed (Devlin, Introduction to Mathematical Thinking).
For my most challenging students, the issue wasn't so much as getting them to communicate their mathematical ideas well, but getting them to communicate at all. For students with extremely low level English ability, being afraid to speak or ask questions in class was a huge roadblock in developing a good grasp on the mathematics we aim to study. The most frustrating times were when students didn't even bother to try. Perhaps this has something to do with being in a culture where "saving face" is important, but students were sometimes so afraid of being wrong that they left entire test pages blank, multiple choice even! (Yes, I know, I was stunned!) You've probably heard this a million times but I'll say it again, mathematics is not a spectator sport! You have to do it to get it, like riding a bicycle. (Am I preaching to the choir here?)
My biggest goal this semester is to get students talking more. About mathematics. In English. A large part of my success will depend on how well I set up a classroom culture of trust and acceptance. This is huge. If I have any hope of getting students to share their original thoughts and ideas they need to know they are safe doing so. Luckily, I've got some ideas to help me get started, but the rest will be trial and error (as is most of my teaching anyway). I also plan on working in a slower progression at the beginning of the year to first get students acquainted with some of the language used to describe mathematical expressions before we dive into what exactly mathematics is. With any luck, every student will be able to describe, in English, what we are learning in any given unit.
Things That Went Well in Semester 1
1) I finally found a groove! Lesson planning no longer takes up hours and hours each day (#win), and I also have a nice support network of experienced teachers to draw ideas from and borrow resources from. Establishing daily routines early on in my classroom (and enforcing them!) also worked wonders.
2) Brain breaks. I was a little hesitant about these at the start since they seemed silly and unnecessary if the lesson is well-chunked. I learned early on though, not all lessons are made equally and some days really are a drag, especially when are teaching 80 minute blocks. Taking a short 5-10 minute break to stretch/play a game/go on your cell phone provides both myself and the students some much needed refuge from a long period of work.
3) First week activities. As I mentioned earlier, setting up a warm and inviting classroom culture is key to being able to get students to talk more math, and learn more in general. I spent about a week doing activities and playing games related to math with my students last semester before I started diving into teaching any curricular content. I plan on spending about the same amount of time, if not more, this coming semester settling in with my new classes.
I'm teaching high school math (grades 10 and 11) this year. My school runs on 80 minute blocks. Here's what I did.
Algebra Seat Finders and Visibly Random Groups - Rather than making a seating plan or having students choose their own seats I greet students at the door and hand them each a card as they walk in. On the card are algebra problems involving one or two step equations and order of operations that are easily solvable via mental math. The answer to the question will tell them which table to sit at. I've arranged my tables into groups of four and have signs taped to the side of the desks so they can easily find the group number. (If you would like to download copy of the seat finder cards I used, they are available at the bottom of my post).
I do the same thing each day, so that every day students will sit in different groups. I like this activity because students are doing math as SOON as they enter the classroom. Some students will cheat and trade cards with other people so they can sit with their friends, but you will come to notice this quickly. I tell students that in this class we are a community and that they will always be working with different people so they get to experience different perspectives and meet everyone in class. Even if certain students don't get along, it's low stakes because the seating changes every day. On Fridays I give them a break and tell them to sit anywhere they like. It was interesting for me to notice that given the choice, students tend to sit with classmates with similar level. Peter Liljedahl has done some cool research on visibly random grouping, check out his free webinar here.
- Bell Work - Who I Am
- Start the class with low key student profile sheet from Dan Meyer as I take attendance. Gives students a chance to tell me about themselves. My favourite questions on this sheet are the "Self Portrait" and "Qualities of a good math teacher.
- Numbers Quiz
- Adapted from Sarah Carter. I beef this up a bit and use this as an opportunity to talk about test/quiz expectations (no talking, no asking a neighbor to borrow an eraser or calculator...etc.), and the consequences for cheating. I tell them that this is a difficult quiz and so far no one has been able to obtain a perfect score. All I ask is for them to try their best, and if they don't know an answer, guess. When I tell them to flip their papers over I usually hear a few chuckles or giggles. Again, I enforce that the room should be silent and let them know I mean business.
- Student Quizzes
- Next, I give them a chance to write ME a quiz about themselves. I take their quizzes and return it to them to be marked. Most students asked basic questions like "What is my favorite subject?" or "What is my favourite food?" Others were more creative and decided to have a bit of fun with the activity...
- Personality Coordinates (Dan Meyer)
- Originally planned to complete this activity the first day, but I was over-ambitious with my planning so ended up introducing it and coming back to it later. First I showed students this diagram:
Student A: What do you notice about this picture?
Student B: I notice there are two perpendicular lines. What do you notice?
Student A: I notice the four dots are arranged in a square. What do you wonder?
Student B: I wonder what the teacher will ask us to do with this diagram. What do you wonder?
Student A: I wonder if this is a function.
..etc.
We discuss and review parts of the coordinate plan. I ask them a few questions about the dots. (Which two dots share the same x-value? Which dot has the lowest x and lowest y value? etc.)
The next time we revisit this activity I start with an example:
- Name Tents (Sarah VanDerWerf)
- At the end of each class on the first week I asked my students to choose ONE question and answer it in their name tents:
- 1. One thing you enjoyed about today's class?
- 2. One question you have.
- 3. A suggestion for class.
- I write back to them every day. This is a big commitment but worth the time in my opinion.
- Some positive feedback I've gotten: Fun, engaging class, students enjoy group work and team activities
- Some things I need to work on: talking slower, writing bigger on the board
- Some questions I've been asked: When do we get the textbook? When do we have our first quiz? Is math difficult?
- At the end of each class on the first week I asked my students to choose ONE question and answer it in their name tents:
- Syllabus Quiz
- Rather than giving a long speech about course expectations, school and class policies, I wrote a quiz. Even though I assign syllabus reading for homework most students will not do this. The quiz is open book and is graded (can be done in pairs), and I count it towards their "English proficiency" grade for the course.
- Talking Points
- This one MUST be modeled to students. It's a little complex, especially for EL Learners so it's important to explain clearly and minimize the amount of instructions given. The main point is to get ALL students talking and sharing their opinions. To model the activity, I pick three random students to do a "practice round" with me. This was less effective with my grade 10 students as they are new to the immersion program. Next semester I might film a teacher example of this activity to show students instead.
- What is Math?
- Share our ideas of what math is, give a common definition of mathematics that we will use for the course.
- Expectations for the Year
- Go over things like: cell phone policy, asking to go to the bathroom, materials needed for class, binder expectations, course evaluation...etc.
- Name Tents
- Again, end the day with student writing me some feedback.
Teach some content and continue reviewing and practicing start of class and dismissal routines.
| Algebra Seat Finders - Groups | |
| File Size: | 16 kb |
| File Type: | docx |
It's personal.
Books like First Days of School and Teach Like a Champion have been invaluable reads, providing tons of practical advice teachers can implement right away. The issue is learning how to filter that knowledge so that it's true to your own teaching style and well-suited to who your students are. Teaching math in an academic classroom is way different than in a college or applied-level classroom, for instance, and not because the material is different per say, but because the students' attitudes towards math differ tremendously. I found that students who are in applied or college-level math courses generally have lower confidence in their math abilities. Subsequently, each wrong answer means another failure added to the list and just reinforces what they already knew, "I'm not good at math." Here, priority #1 is to build a safe and welcoming classroom where a culture of error is the norm, and is celebrated as a vehicle for learning. Likewise, North American students and Asian students also differ in their attitudes towards math. Comparatively speaking, math anxiety seems to be a bigger issue in North America. On the other hand, students in Asia tend to be really good at math, they respect the subject, and they will work hard at it, even when things get tough. In Asia, the norm is repeat and rehearse everything the teacher's taught, but the challenge is to get kids thinking independently and creatively.
Different mindsets on math, as told in memes:
April's Tips on Classroom Management
 The answer is probably yes.
The answer is probably yes. 0. Plan a good lesson. I'm echoing Fawn on this one when I say that having an engaging lesson solves soooooo many potential discipline issues in the classroom. Kids will act out when they are bored. I know this because I WAS this. I mean, I was an A student throughout high school and a MODEL student at that. One summer I took a physics and had a teacher who literally read the textbook to us. I can do that myself, thank you very much. So, rather than sit in silence and boredom, I discovered that the reflective properties of light were pretty fun to play around with. I was particularly intrigued at how various angles of light rays from the window would bounced off the shiny surface of my watch right into - yup, the teacher's eyes.
1. Learn names. I always make it a point to know the names of all my students and connect with them in some way. To me, there's nothing worse than being called "you in the red shirt" or "hey you." Teach students, not the subject.
2. Don't repeat student answers. I first noticed this during my observations of a veteran teacher while I was student teaching, and it completely changes the way discussions flow in the classroom. If a student answers a question, and the teacher repeats the answer (usually in a louder voice or with elaborations), in the students minds this translates to, "Information is not important, unless it comes out of the teacher's mouth." If a student says something really insightful, ask them to repeat it instead - you'll have reinforced two important messages to a) the student: "Your contributions are valuable!", and b) the class, "We have a lot to learn from our peers!" It is so vital for teachers to give students opportunities to be responsible for their own learning.
3. No Opt-Out. I got this one from Teach Like a Champion. The premise is simple, if a student does not know the answer to a question, they cannot get away with "I don't know." You might ask another student for their thoughts, you might provide a hint, you might just say the answer outright, but you will always go back to the student who said, "I don't know." "I don't know" is not an acceptable answer in my classroom. We want students to get from:
"I don't know" therefore "I don't have to try", to
"I don't know, YET" so "I'm going to keep trying."
4. Keep it simple. If you're like me, you probably have a list of 20 different procedures, routines, and policies you'd like your students to do and maintain throughout the year, but this is not realistic! I ended up flopping on most of them. My first two years of teaching have been chaotic, and I'm slowly coming to accept that it will be this way for a while. Focus on the five most important guidelines and procedures that your classroom cannot do without, then build from there.
5. Document everything. The biggest lifesaver for me last year was getting students to fill out "Action Plans" for whenever they made a bad choice. There are many variants of this on Pintrest. Student Responsibility Cards for homework were also cool, but didn't work out that well for my classroom because I didn't follow through on consequences. So I'll keep the first and toss out the latter. Links to some documents I used below.
I'm now going into my third year of teaching, and so far, each year has been in a different country, which has made each "first day" even more special.
My First First Day
Subject: Math
Grade: 10
In my very first day of my very first full time teaching job in Kazakhstan (blog post here), I spent the first day getting to know my students, telling them a bit about myself, talking to them about my expectations for the class, taking selfies of all the students, and giving them some general advice about how to succeed in math class. I found that it was important and effective to start building those relationships with my students from day one, and by learning all their names as quickly as possible, I let them know that I notice them and care about them.
Prior to preparing my first day lesson plans, I soaked up as much information as I could with all the resources that were available to me. I had read First Days of School by Harry and Rosemary Wong and a few other teaching books, browsed the internet for countless hours looking for ideas and inspiration, watched this entire video by Agape Management, and looked for elements of each that I thought would be suitable for my teaching style. What didn't work, however, was the fact that I did not start the year knowing where I wanted my students to be by the end of the year. This was difficult because I didn't know much about the culture, the style of teaching that students were accustomed to, and I had never taught a class full of ELL students before (hence why nobody laughed at my jokes). Moreover, I did not have full autonomy over the classroom (it was supposed to be a co-teaching type environment but ended up feeling more like I was "guest teaching" a few times a week); my co-teachers were not fluent in English, and had different visions of how they wanted to run their classrooms, which made it difficult to have consistency when it came to expectations and rules.
What ended up happening was that the first day allowed me to start building relationships with my students, but it did nothing to help me manage my classroom (because nothing was consistently enforced). If I could re-do my first day, I would spend more time getting to know my co-teachers, and specifically, these are the questions I would ask:
1. What are your classroom rules and expectations?
2. What are your beliefs about learning in math? (i.e. How do students learn best?)
3. What are your beliefs about teaching in math? (i.e. How can teachers best reach their students?)
4. Describe a typical day in the math classroom for you.
I learned that it is important not to go in assuming that your teaching partner will have the same views about teaching and learning as you do, and not only that but that I needed to take the time to get to know and understand their views! Had I done so much earlier I would have discovered that hands-on activities, student investigations, or differentiated teaching and learning weren't a common tools in their teaching toolbox. The general style of teaching I observed included very fast-paced progression through the units, with lots repetition and mental computations, but very little time spent developing the concepts or looking at their applications. Knowing this, I would have modified my first day presentation to include some math activities that integrated both styles of teaching.
The Second First Day
Subject: Science
Grades: 8 - 10
In my second year, I taught in South Korea and had full control over my own classroom, which made it significantly easier to plan and organize everything the way I wanted to. My first interaction with my students, however, was not on the first day of class. We had an "orientation day" in which both students and parents attended brief 10 minute presentations by all their teachers.
I began by greeting every student and parent at the door with a handshake. I called the students by name as they walked into the classroom, which took a lot of time for me to learn beforehand, but was so worth the reactions! Prior to meeting all of them, I borrowed the previous years' yearbook and memorized the faces and names of all the students I would be teaching in my classes. Some of them looked stunned that I knew their names already, when none of them had a clue who I was yet!
At the front of the room, I had copies of letter to parents and the course syllabus which I asked each student to pick up as they walked in. In my presentation, I talked briefly about who I was, my educational background, and what students can be expecting to learn this year. My primary goal was to let them know that I care about them and their learning, and that while this year would be challenging, they would also be supported by me.
Then, on the actual first day of class, I had students fill out a "Get to Know Me" form, we played an icebreaker game (two truths and a lie - my favourite to this day), I talked about the rules and expectations, and I ended the day by teaching them my class dismissal routine. What I DIDN'T do (but wish I did), however, was any science, and that's about to change for this year.
This Upcoming School Year
Subject: Chemistry (?), TBD
Grades: 9 - 12 (?) TBD
As in the past, my main goals for the first day of school are:
1) get to know my students, and
2) set the tone for the rest of the year,
but how I plan to achieve them will change somewhat.
1 - Getting to know my students.
Ideally, I would like to learn student names as quickly as I can, before the first day, if possible. But regardless, I would still like to use name tents with feedback, an idea that Sara Vanderwerf talks about in her blog. I think this is a great way to connect with students individually and on a more personal level. I would also like to take pictures of the students with their name tents so I have a visual record as well. A modification I will make to Sara's version of the name tents is that I will provide some open-ended prompts that the students can respond to, so that they have a jumping-off point for organic thoughts to develop. For instance:
- I noticed ...
- I wonder ...
- I learned ...
- I wish ...
I also really like the Talking Points activity from MathMinds and plan to modify it to make it chemistry specific.
Another idea I've been toying with is some sort of homework assignment that addresses a few or all of the 5 Questions to Ask Your Students To Start the School Year from @gcouros but my problem with this is that I don't want it to JUST be about rapport building, it needs to address or be linked an aspect of science (or science learning) specifically... to be determined.
We will, presumably, be doing chemistry so I would like to begin the first day with a demonstration, or an activity related to the nature and processes of science. Some ideas I would like to try:
Stacking Cups (Dan Meyer) - related to concepts of measurement, accuracy, precision, and estimation
Candle Light Activity (Art of Teaching Science) - importance of observation (qualitative and quantitative) in science, making inferences and predictions, chemical and physical properties
Ira Remsen Demo (Michael Morgan) - observation, predictions, inferences, chemical safety, chemical reactions
I believe that it is important to talk about my expectations and what students can expect out of the class, however, what I DON'T want to do is just read the syllabus on the first day. A prof once suggested just letting the students read the syllabus at home and talk about it the following day so they can ask questions about what they read, or doing a quiz if necessary about the content in the syllabus.
First Day Plan (rough draft):
1) Greet students at the door
2) Have an activity for them to get started with on their desk (either to quietly read the syllabus or fill out a Who I Am handout)
3) Introductions myself and the course
4) Student introductions + talking points
5) Do some science!
6) Dismissal routine
Concluding thoughts
My first day experiences thus far have been pretty nerve-racking and exciting. I'm slowly learning to strike the right balance between talking about rules and procedures to relinquishing control, and giving voice to the students. This is particularly difficult in a room full of ELL students, but once they gain confidence in their ability to speak and be heard, I found that they had a lot to contribute. With international schools, it is usually the case that the students are well acquainted with each other already, so usually the introductions are more for the teacher rather than the students. Even though students may already know each other, however, my role as a teacher to facilitate a safe and positive community cannot be ignored. This was made prevalent to me in Korea when I realized that students still felt unwilling to work with particular classmates even though they had been in the same classes for years. Regardless of country, language, or culture, my biggest take away for the first day of the school year is to BUILD RELATIONSHIPS and ESTABLISH COMMUNITY. I will keep this in mind as I continue to plan for my first day of school in China this school year!

Improvising is wonderful. But, the thing is that you cannot improvise unless you know exactly what you're doing
- Christoper Walken
The dream: foster greater teamwork, collaboration, and creativity amongst my students. The reality: a lot of reluctance, awkward silences, and miscommunication. Students were reluctant to participate because it potentially meant making a fool of themselves in front of their classmates. There were awkward silences because they were uncomfortable with the idea that they could control the dialogue rather than do what they were told. Miscommunication happened because students focused too much on making themselves look good at the cost of sloppy scene work.
Our first attempts at simple improv games failed tremendously. The foundation of trust wasn't there, and students had not yet learned the art of failing spectacularly. I challenged my students often and constantly pushed them towards more complicated tasks and scene work. What I didn't realize, however, was that my students probably needed a much gentler progression, and more scaffolding. If I were to teach improv again I would spend more time on the fundamental concepts and revisit them often. I would tell my students that you don't need to be loud to be heard, and I would focus more of my feedback on things that were going well rather than things that weren't.
Even though my little experimentations with improv failed in a lot of ways, I learned much from the experience and would do it again in a heartbeat. Not only did teaching improv put me out of my comfort zone in terms of teaching, but we had a lot of fun! In the beginning I did a lot of "telling"; I read up on the rules and common pitfalls and communicated these to my students in hopes that they would avoid them. This did not work. They did those things anyway. But they got really good at doing those things, so for half a class, we just practiced doing scenarios in which your partner either blocked or wimped* in a scenario and we talked about what that felt like and how to make it better. Then we tried adhering to the "yes, and" rule and discovered that it was harder than it seems! With repeated trials and errors, we slowly progressed to a point where a few students felt comfortable performing on stage, others began to feel a little less intimidated, and everyone learned a bit about what it means to work together effectively.
Teaching and learning about improvisation was like figuring out how to have a great conversation. When a scene goes poorly, it is usually because a player is too much in their own heads and not focused on their scene partner. Much like in life, this is annoying because we seldom have great conversations with people who try to make everything about themselves. As we continued to explore improv, both my students and I became more mindful of how certain responses can either help or hinder a scene. A friend of mine gave me some good improv advice, "You should always make your partner look good," which is another way of saying, "This isn't about you." For example, your scene partner makes an offer and says, "Wow, the view is amazing from here," and if you say, "What view?" then you are putting a lot of pressure on your partner to make something up to progress the scene. If instead you respond, "I have really bad vertigo, I need to get off this cliff," then you just made your partner look good by taking their offer, and adding some valuable information to it.
Wouldn't it be great if all class discussions could flow so smoothly? Where all students are equal participants, building on the ideas of one another, and each adding something of value? I see value in teaching and learning improv outside the drama classroom. This article makes some good arguments for why and how improv can be incorporated into all subject matters, and has some great sample games and activities that can be modified for all grade levels. If you are a teacher who is curious about how improv can be implemented into other subjects, I highly recommend reading this paper.
Below are a list of Tina Fey's four basic rules on improvisation, taken from her book Bossypants. In my next blog, I will elaborate on how I believe these rules are connected with my teaching practice.
Example
Player A: Look at that dog!
Player B: What dog?
Wimping: Accepting an offer but failing to act on it.
Example
Player A: We should go to the movies.
Player B: Yes.
More info here.
1. Build a thinking classroom.
This isn't a new goal for me, but something I'm always trying to do better. In teacher's college, I was introduced to the phrase "Explore First, Explain Later" in my Introduction to Biology Teaching class and this is something I try to incorporate into my math and science classes every single day. The concept is self-explanatory; students are given a chance to explore, investigate, and uncover ideas within a particular topic or concept prior to taking formalized notes. This teaching methodology is congruent to the constructivist theory of learning which states that "that learning is an active, contextualized process of constructing knowledge rather than acquiring it" (learningtheories.com).
"Exploration" can take many forms; investigation, experiments, noticing and wondering... however, something I'm keen on devoting more time to in my planning and lessons is developing the question. Daniel T. Willingham writes about this in his book Why Don't Students Like School, "Sometimes I think that we, as teachers, are so eager to get to the answers that we do not devote sufficient time to developing the question." I've really been following Dan Meyer's lead on how to do this; his blog post on "The Three Acts of a Mathematical Story" are a good place to start.
Peter Liljedahl also hosts a free webinar on how to build a thinking classroom, available here.
It is so easy to just fall into a routine of lecturing/note-taking followed by independent (usually textbook) work, but I eventually want to create an environment in which students manage themselves. This begins by getting them to talk more, exchange ideas, and share what they already know. Some things I'm excited about trying in my classroom are Stand and Talks (Sara VDW), and talking points (adapted from Lyn Dawes).
3. Do fewer things better.
When I first started my student teaching, it consumed my life. Go to school, plan for the next day, sleep, and repeat. I stopped exercising, watching TV, hanging out with my friends... and basically anything that was not work-related. I could've used an old lesson plan my associate teacher has taught before; I could've downloaded lesson resources online; or I could have picked one really good question and focus the class on that for the entire period. There were a million things I could have done better, but no. Instead, I scoured dozens of sites for lesson ideas, worksheets, and activities before creating my own unique cocktail using an amalgamation of the best ideas I had gathered. I made my own worksheets and presentations because I wanted things done in my own exact, particular way. Planning a single lesson would take me hours - this is not sustainable!
I know better, so I'm going to do better this year. Angela Watson's keynote presentation for the Build Math Minds Virtual Summit really helped me refocus and re-evaluate my priorities. I'm going to invest my energy in doing the stuff that matters, and NOT because:
- Of peer pressure "Everyone else is doing it, so I'd better do too!"
- It's tradition "We do this every year, so we must do it this year!"
- It's instagram-worthy "OMG this will look so cute when it's done!"
Instead I'll only commit my energy to doing something if:
- It will help me help students engage and interact with the subject in a meaningful way
- I believe it is the best use of my students' class time
- It is something I am genuinely excited about trying in my classroom
Three things I'm going to start doing now to achieve this goal:
1) Manage my time by setting a timer for the tasks that need to get done, and stick to it. Whatever gets done during that time doesn't have to be perfect or have beautiful fonts and layouts, it just needs to be good enough.
2) Reduce my workload by only formally assessing student work if I believe it is a TRUE reflection of student learning.
3) Increase efficiency by delegating tasks to students, like self-marking formative assessments.
In science, one of the first activities I do with my students is have them sketch an image of a scientist. That's it. The activity is simple but reveals a lot about our preconceived notions of what science is and what exactly it is that scientists do. The stereotypical image of a scientist is presented as follows: a white male with wacky hair in a white lab coat working in a laboratory with chemistry equipment. We talk about what these stereotypes mean and where they come from. We talk about why these images are problematic and what we can do about it. And then, we revise.
- Two identical Lego sets per group (I would recommend no more than 20 pieces per set as the focus should be on the procedure writing rather than the Lego building)
- Student Handout: Designing a Procedure
- Cardboard boxes (or some other material that can be used as a shield)
| designingaprocedure.pdf | |
| File Size: | 93 kb |
| File Type: | |
I started the lesson by asking students two questions:
- What is a procedure?
- When do we use procedures in our everyday lives?
Explore
PART 1: Designing the Structure and Writing the Procedure

Explain
After students had a chance to follow another group's procedure, they completed question #5 in Part II of the student handout (above). Once the students have had time to write down their thoughts I had them share their feedback with the other groups.
Notes: Some students began to get overly critical and picky about each other's procedure. At this point, I reminded them of what constructive feedback looks like, and reminded them that mistakes are OKAY - they are part of the learning process.
Extend
An extension might be to have students follow-up this activity with a procedure about making a peanut butter and jelly sandwich, brushing their teeth, or some other common, everyday task.
Note: This would also be a good time to discuss how scientific procedures differ from everyday ones, and how the formatting may change depending on the class. For example, in my class, students will be expected to write their procedures in past tense and include labeled diagrams with figure captions written below the diagram.
Evaluate
I will evaluate my students on their ability to write clear, accurate, and reproducible procedures as a part of their Mystery Solids Investigation performance task.
April Soo
International math educator who writes, occasionally.
Archives
April 2020
March 2020
February 2020
January 2020
July 2019
June 2019
January 2019
September 2018
August 2018
July 2018
April 2018
January 2018
September 2017
August 2017
July 2017
June 2017
February 2017
November 2016
October 2016
August 2016
June 2016
May 2016
April 2016
March 2016
February 2016
January 2016
December 2015
October 2015
September 2015
August 2015
July 2015
June 2015
May 2015
February 2015
January 2015
December 2014
August 2014
July 2014
Categories
All
Books
Calculus
China
Classroom Management
Counting
Escape Room
First Day
First Week
Goals
Improv
Inspiration
Inverse Functions
Kazakhstan
Learning How To Learn
Lessons
Life Musings
Make It Stick
Map Projections
Math
Math Journals
Mindset
MMT
#MTBoS
Myanmar
My Teaching Journey
Naked Statistics
Permutations
Polynomials
Probability
Reflections
Science
Silent Teaching
Sketch A Scientist
Student Teaching
#sundayfunday
Symmetry
Teaching Drama
Teaching Tips
Videos
Why Math?
Writing Procedures
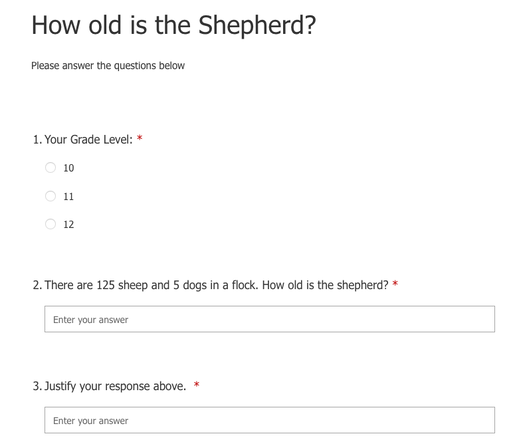




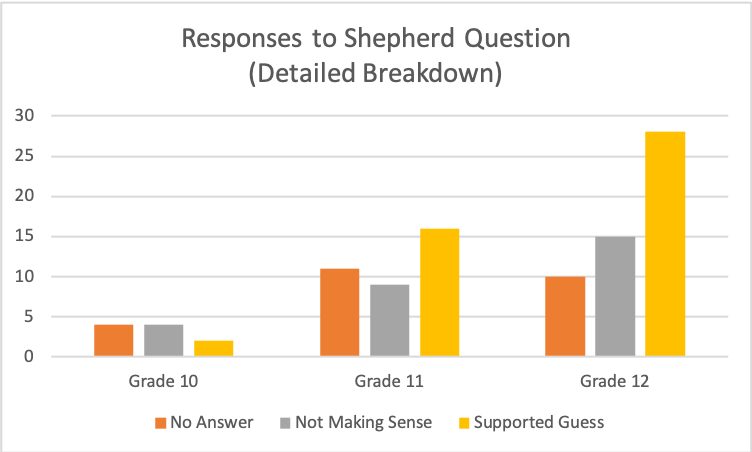
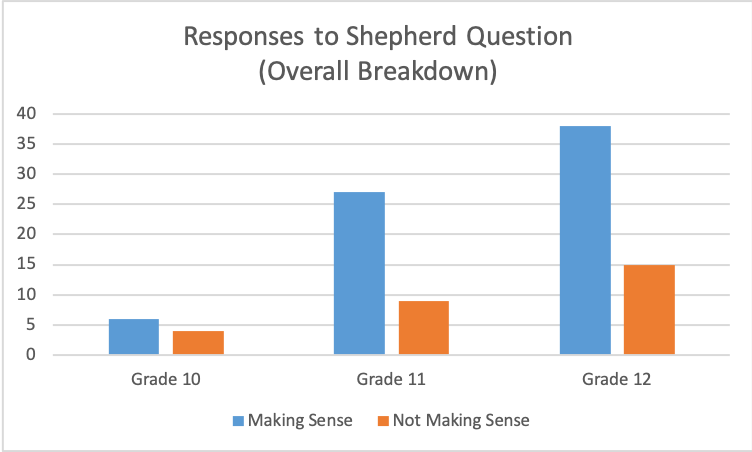

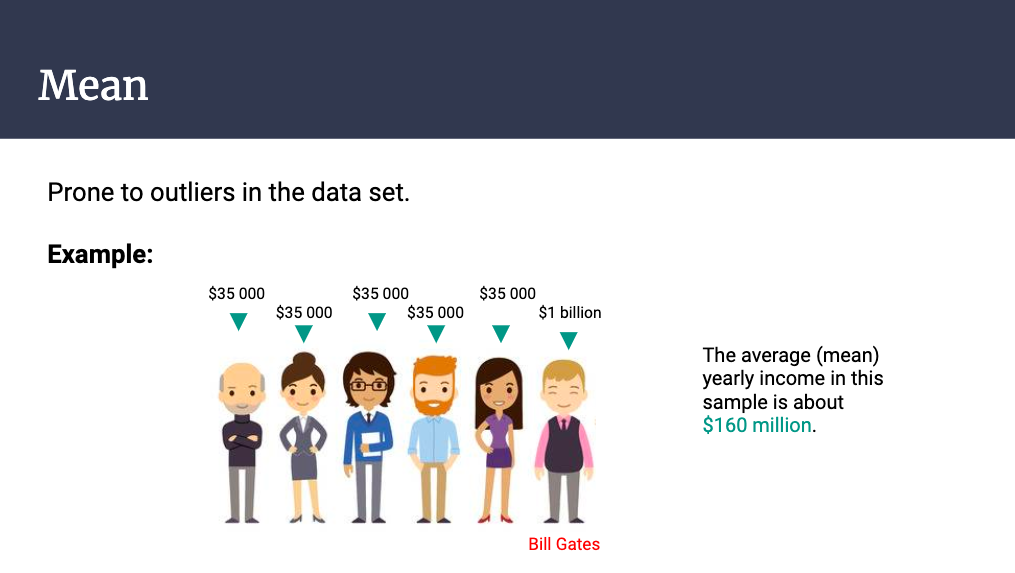




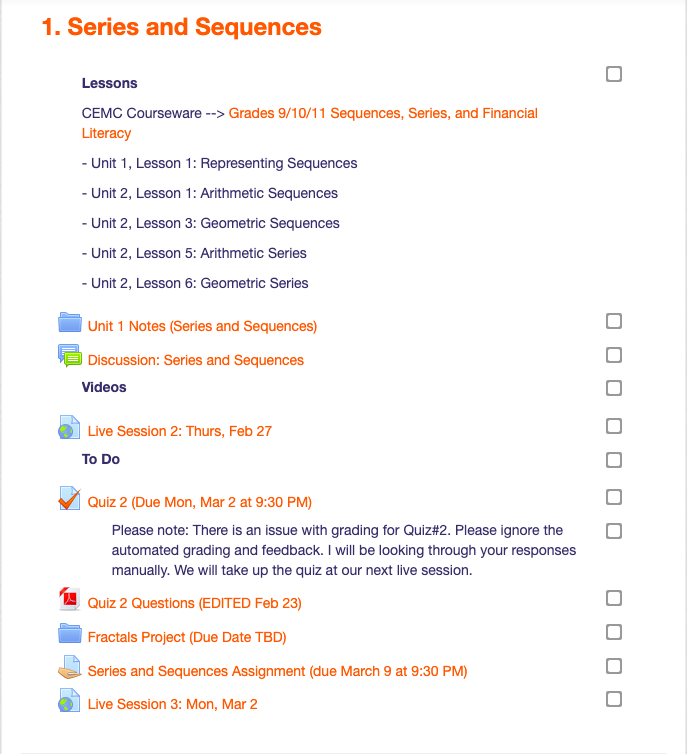
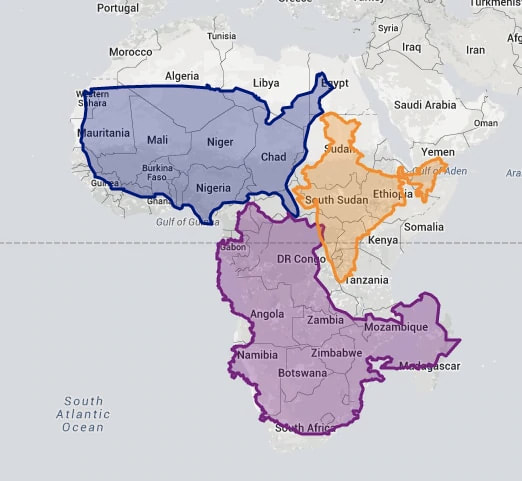

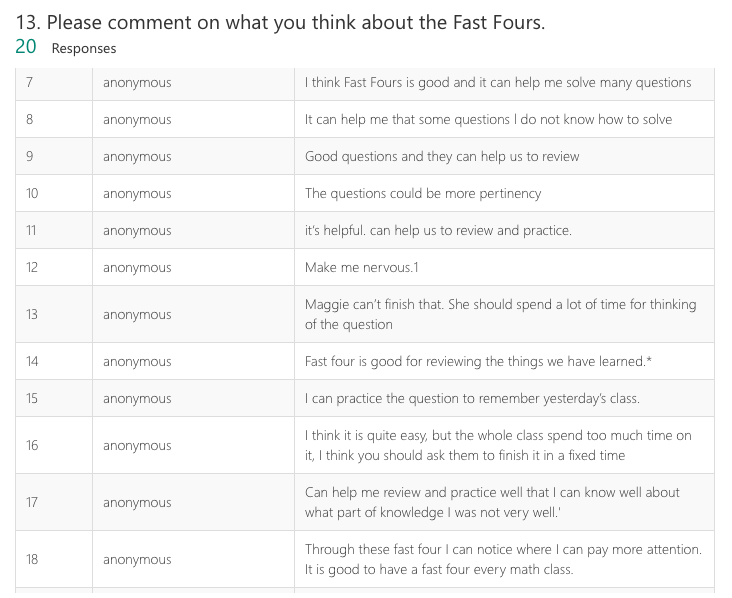
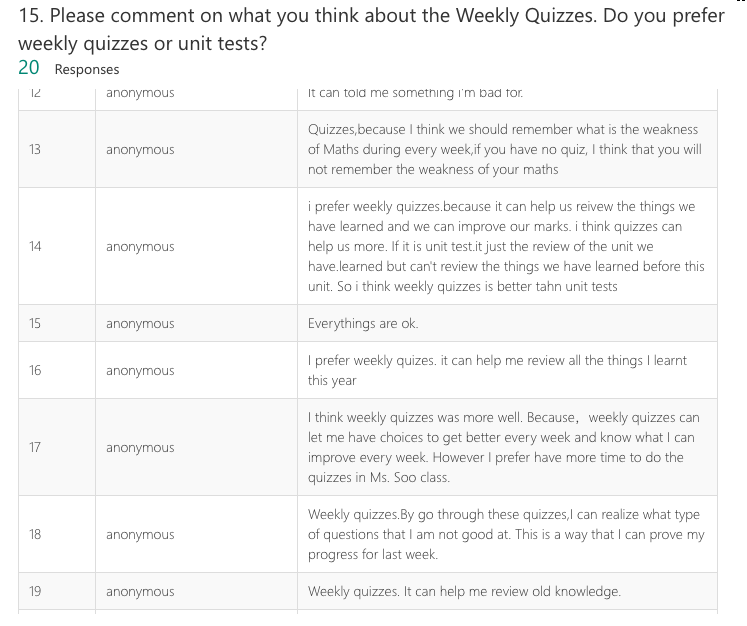



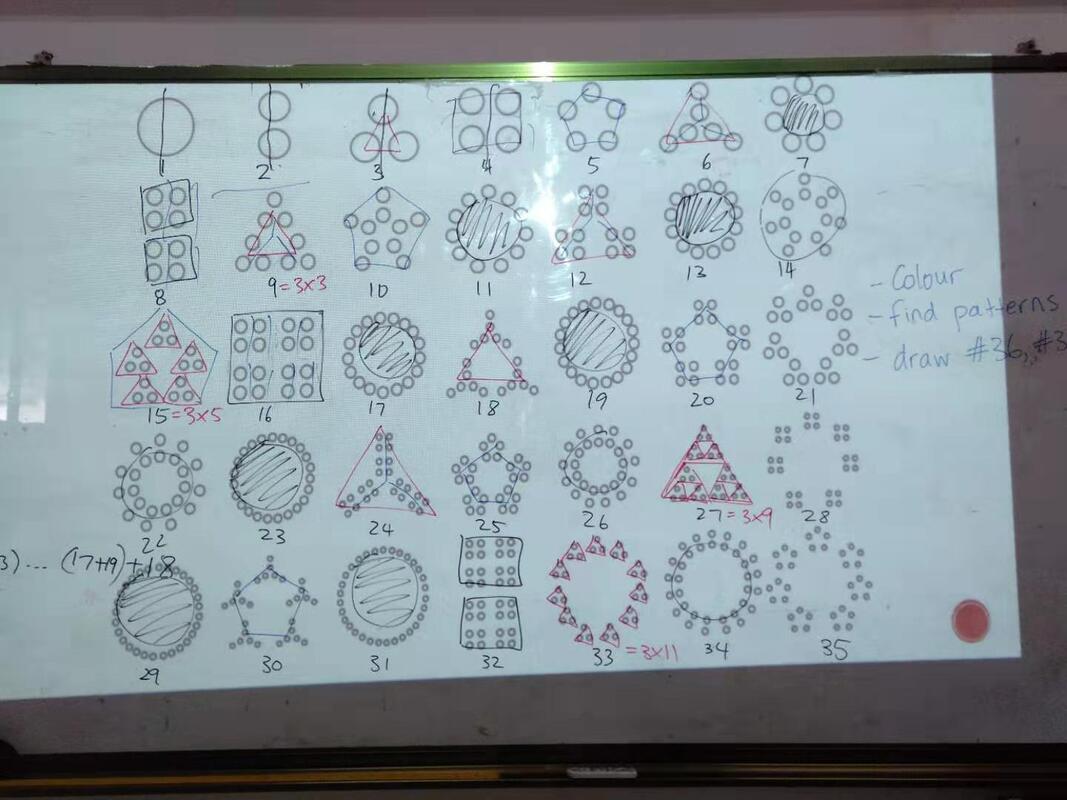


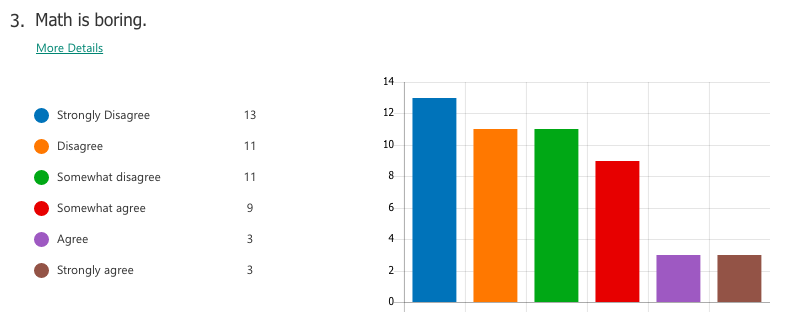
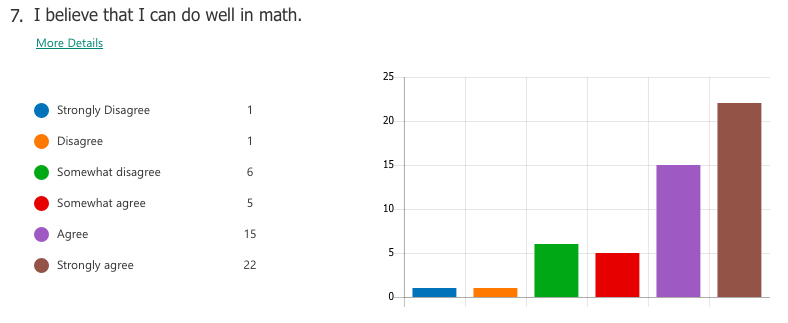
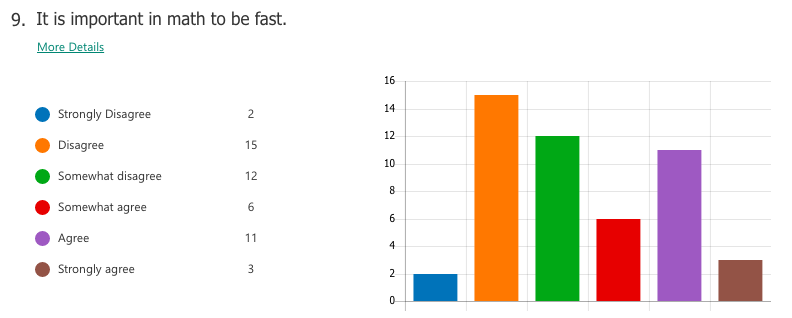
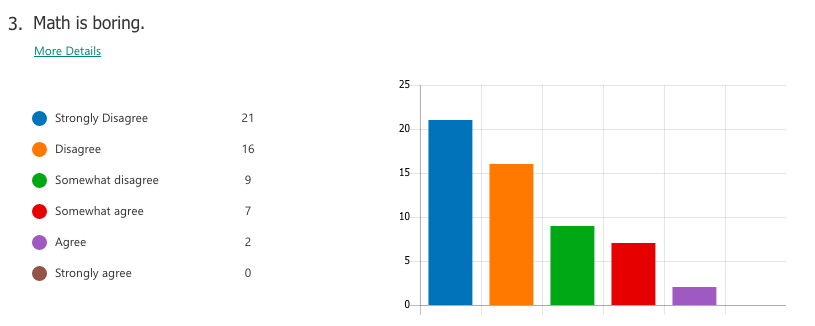
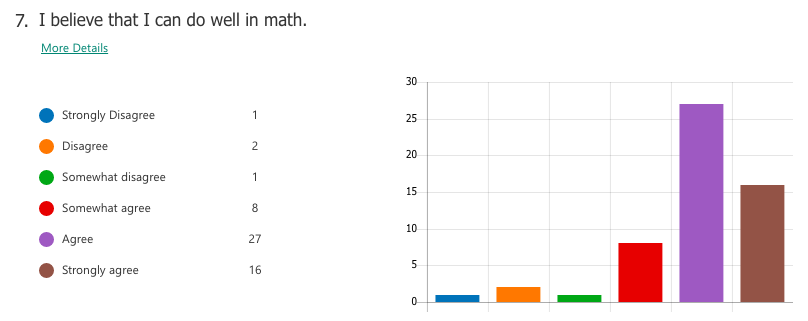
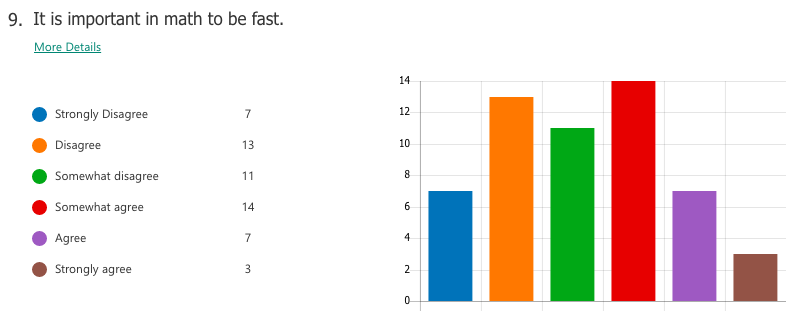
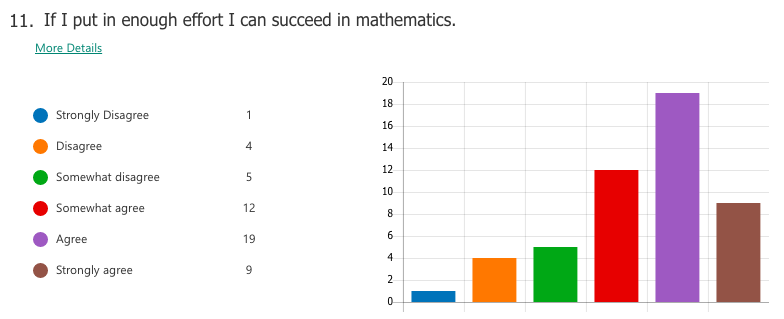
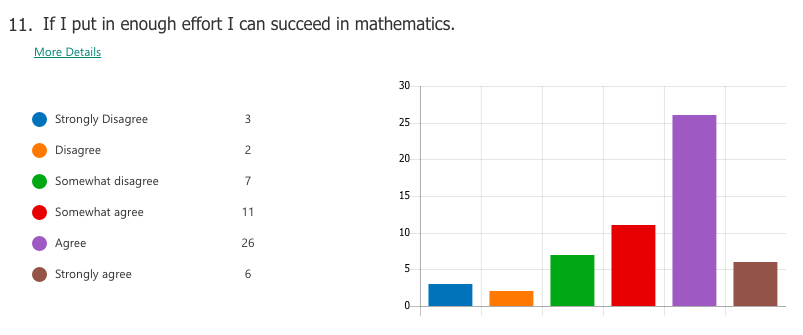
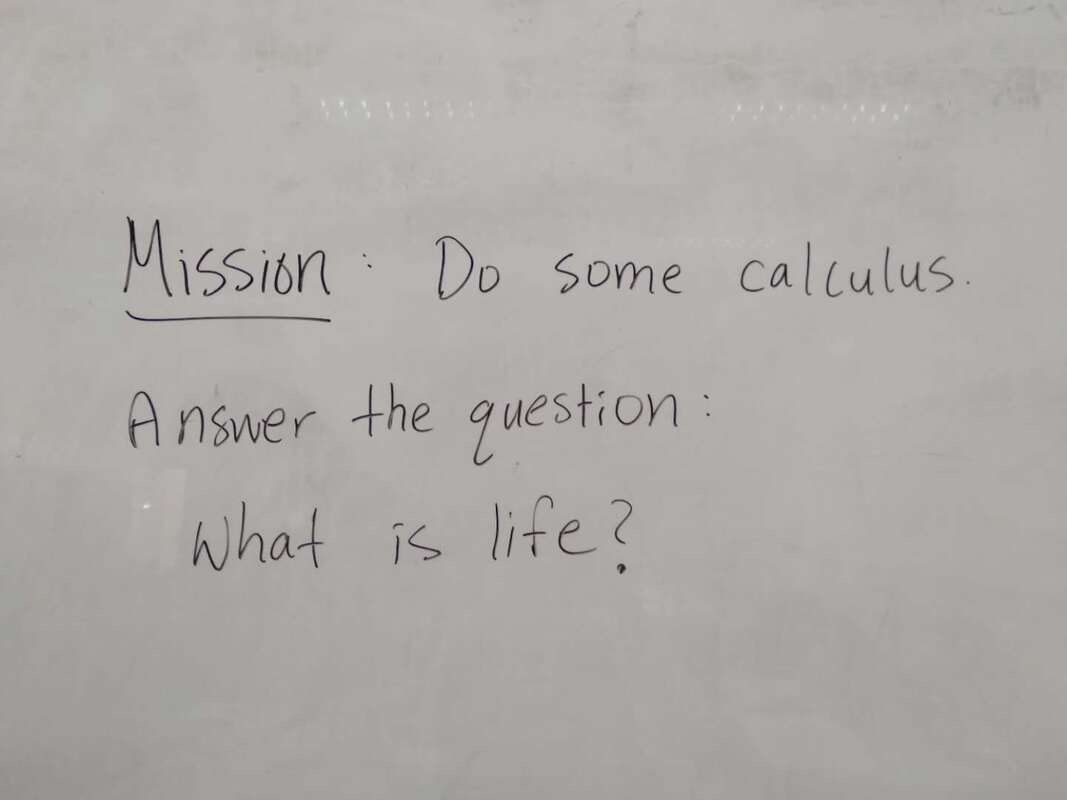





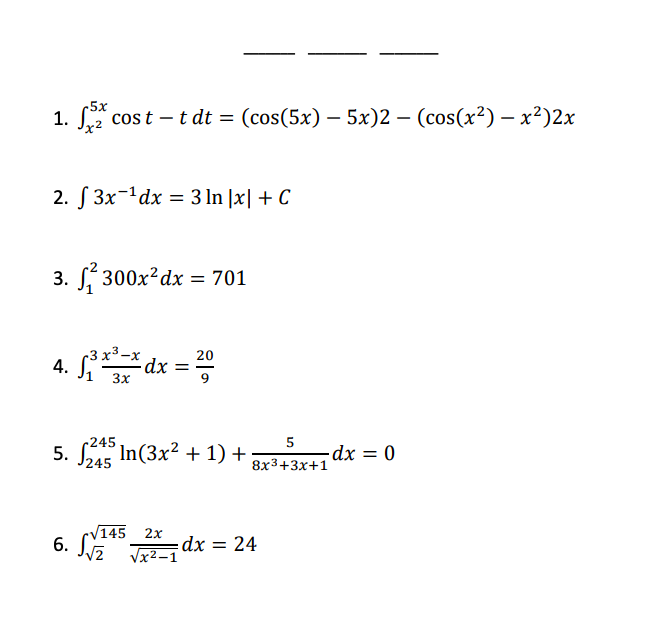






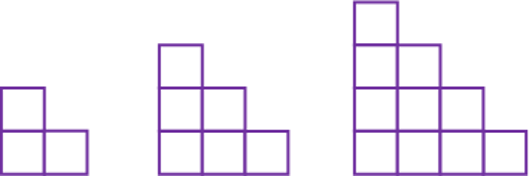
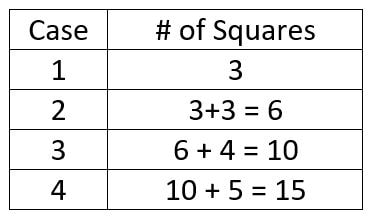
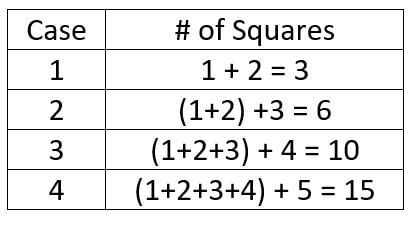
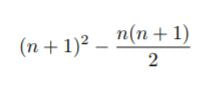
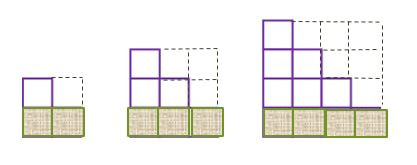
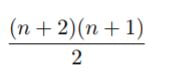
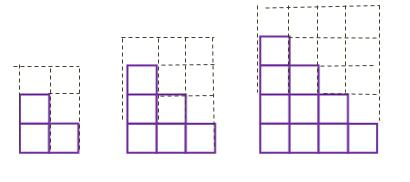

























































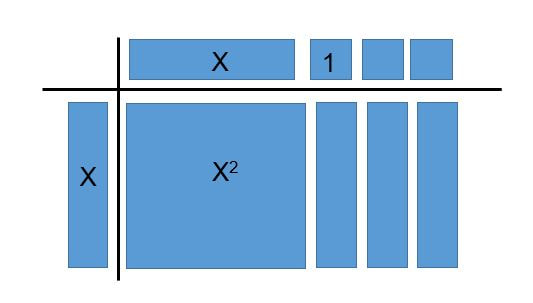








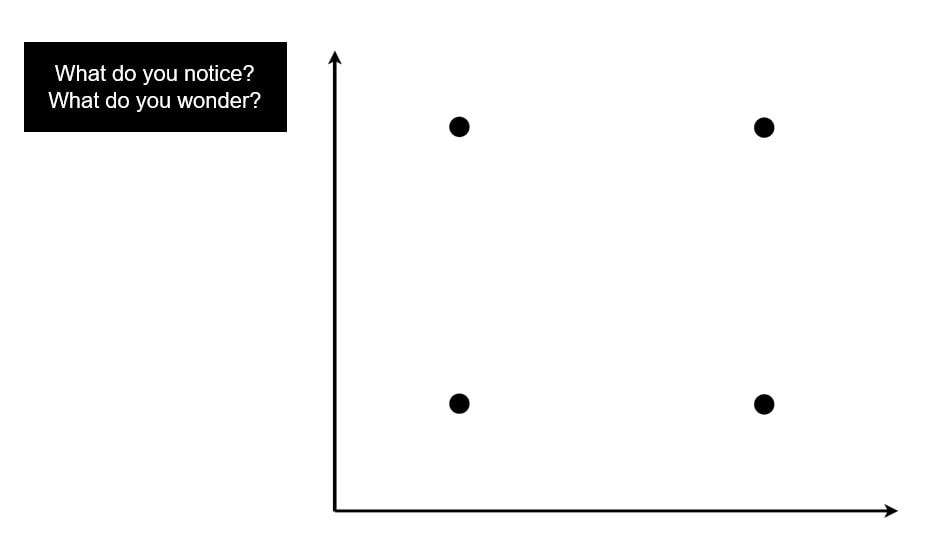
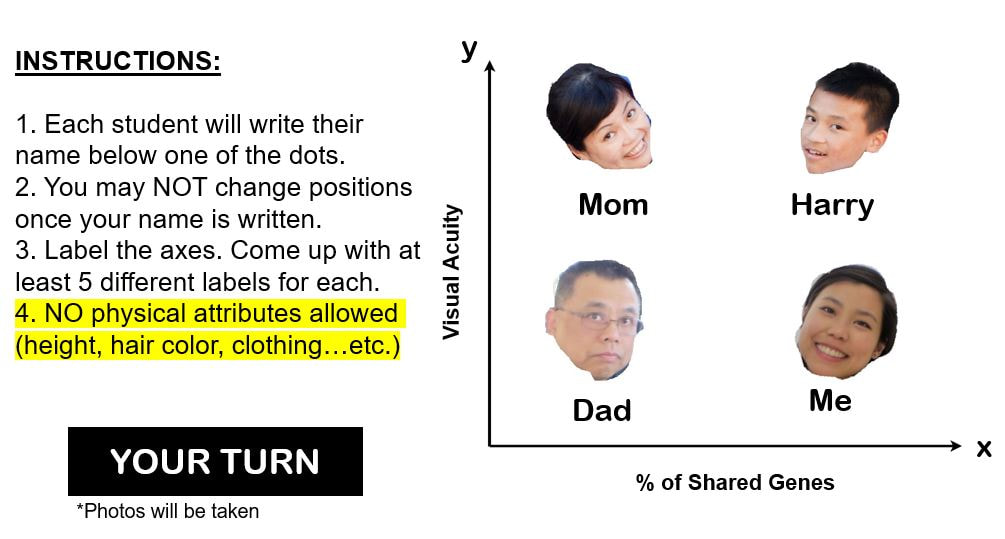
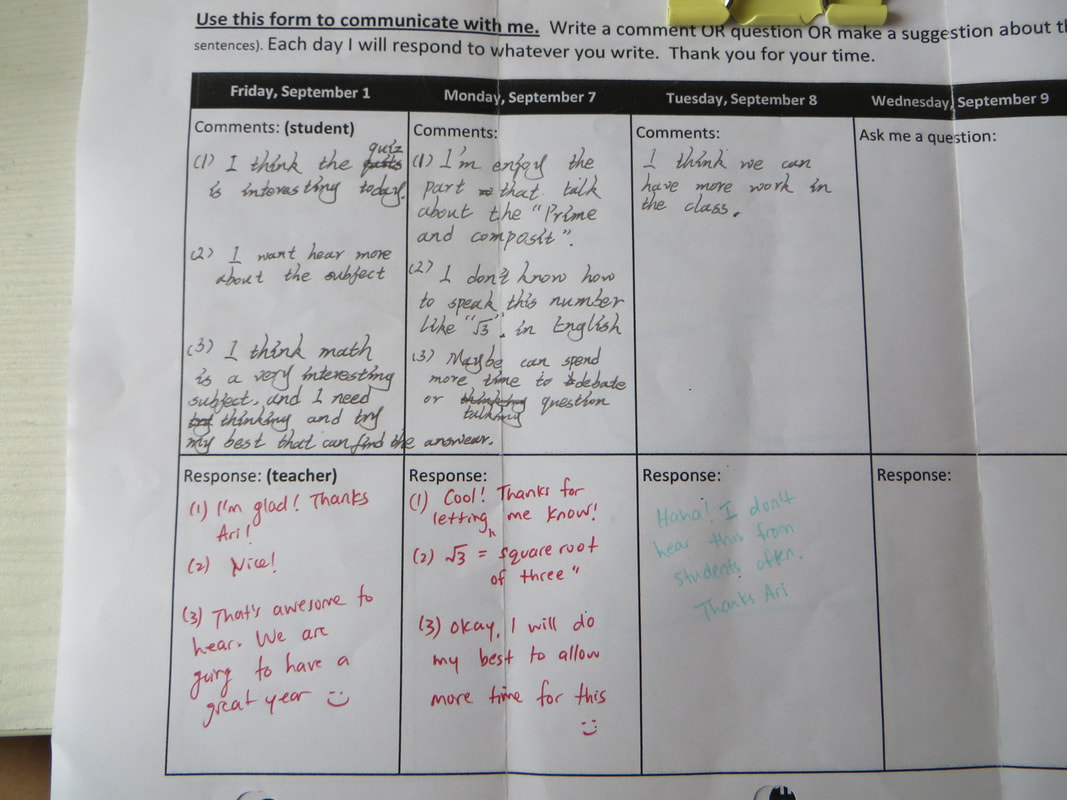















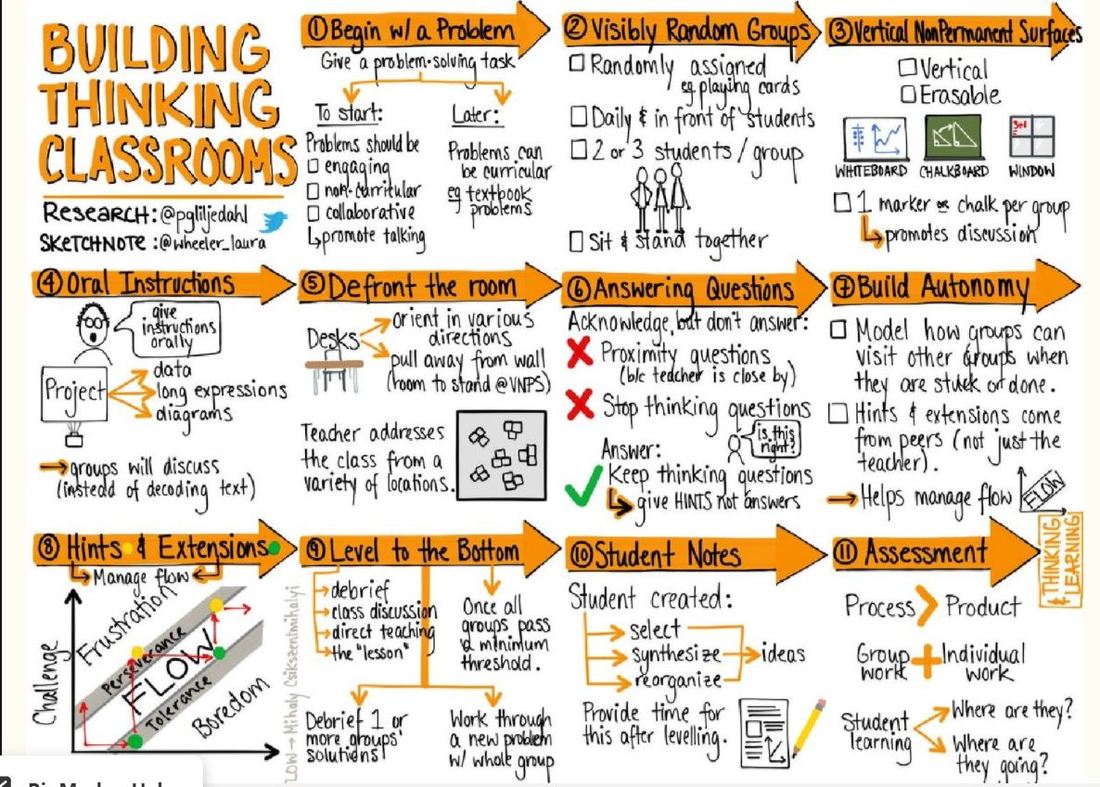














 RSS Feed
RSS Feed
