|
Semester one of my first year living and working in China is officially over! Since my last post about the first day of school, I realized haven't blogged at all this entire semester. I am a little disappointed that I had skipped through all the middle bits, but regardless, here we are.
This past semester I taught Math 10 and 11 of the British Columbia curriculum at an international school in Suzhou, China. With the exception of a handful of students, all of them are English Language Learners. Some might argue that this does not pose a big problem in mathematics, since the language of mathematics can be viewed as a combination of abstract signs and symbols separate from the English language. The problem is, it is one thing to understand mathematical ideas and concepts, but another to be able to communicate them. Someone who is well versed in a mathematics should theoretically be able to describe the same concept in more ways than one - numerically, algebraically, graphically, and verbally. Mathematicians strive for precision in expressing ideas, and this is not always simple. Aside from students having to approach mathematics from an ELL standpoint, the issue is compounded when you consider all the ways in which ambiguity arises in the English Language. Take for instance the word "and"; conjunction in mathematics is commutative (A^B is the same as B^A), but you can see from the example below that "and" in everyday English is not commutative. The sentence, "John took the free kick, and the ball went into the net," would have a very different meaning if the conjuncts were reversed (Devlin, Introduction to Mathematical Thinking). For my most challenging students, the issue wasn't so much as getting them to communicate their mathematical ideas well, but getting them to communicate at all. For students with extremely low level English ability, being afraid to speak or ask questions in class was a huge roadblock in developing a good grasp on the mathematics we aim to study. The most frustrating times were when students didn't even bother to try. Perhaps this has something to do with being in a culture where "saving face" is important, but students were sometimes so afraid of being wrong that they left entire test pages blank, multiple choice even! (Yes, I know, I was stunned!) You've probably heard this a million times but I'll say it again, mathematics is not a spectator sport! You have to do it to get it, like riding a bicycle. (Am I preaching to the choir here?) My biggest goal this semester is to get students talking more. About mathematics. In English. A large part of my success will depend on how well I set up a classroom culture of trust and acceptance. This is huge. If I have any hope of getting students to share their original thoughts and ideas they need to know they are safe doing so. Luckily, I've got some ideas to help me get started, but the rest will be trial and error (as is most of my teaching anyway). I also plan on working in a slower progression at the beginning of the year to first get students acquainted with some of the language used to describe mathematical expressions before we dive into what exactly mathematics is. With any luck, every student will be able to describe, in English, what we are learning in any given unit. Things That Went Well in Semester 1 1) I finally found a groove! Lesson planning no longer takes up hours and hours each day (#win), and I also have a nice support network of experienced teachers to draw ideas from and borrow resources from. Establishing daily routines early on in my classroom (and enforcing them!) also worked wonders. 2) Brain breaks. I was a little hesitant about these at the start since they seemed silly and unnecessary if the lesson is well-chunked. I learned early on though, not all lessons are made equally and some days really are a drag, especially when are teaching 80 minute blocks. Taking a short 5-10 minute break to stretch/play a game/go on your cell phone provides both myself and the students some much needed refuge from a long period of work. 3) First week activities. As I mentioned earlier, setting up a warm and inviting classroom culture is key to being able to get students to talk more math, and learn more in general. I spent about a week doing activities and playing games related to math with my students last semester before I started diving into teaching any curricular content. I plan on spending about the same amount of time, if not more, this coming semester settling in with my new classes.
0 Comments
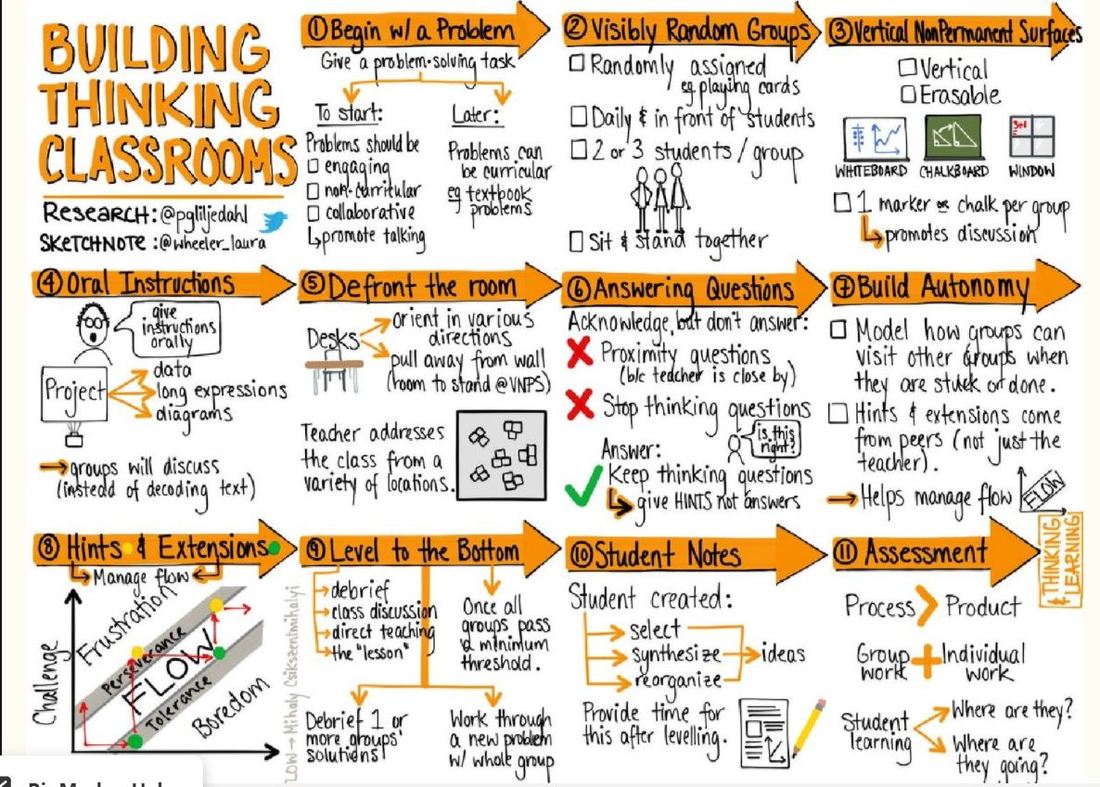
I'm participating in the #sundayfunday blogging initiative within the #MTBoS community. More info here. 1. Build a thinking classroom. This isn't a new goal for me, but something I'm always trying to do better. In teacher's college, I was introduced to the phrase "Explore First, Explain Later" in my Introduction to Biology Teaching class and this is something I try to incorporate into my math and science classes every single day. The concept is self-explanatory; students are given a chance to explore, investigate, and uncover ideas within a particular topic or concept prior to taking formalized notes. This teaching methodology is congruent to the constructivist theory of learning which states that "that learning is an active, contextualized process of constructing knowledge rather than acquiring it" (learningtheories.com). "Exploration" can take many forms; investigation, experiments, noticing and wondering... however, something I'm keen on devoting more time to in my planning and lessons is developing the question. Daniel T. Willingham writes about this in his book Why Don't Students Like School, "Sometimes I think that we, as teachers, are so eager to get to the answers that we do not devote sufficient time to developing the question." I've really been following Dan Meyer's lead on how to do this; his blog post on "The Three Acts of a Mathematical Story" are a good place to start. Peter Liljedahl also hosts a free webinar on how to build a thinking classroom, available here. 2. Get students to talk more.
It is so easy to just fall into a routine of lecturing/note-taking followed by independent (usually textbook) work, but I eventually want to create an environment in which students manage themselves. This begins by getting them to talk more, exchange ideas, and share what they already know. Some things I'm excited about trying in my classroom are Stand and Talks (Sara VDW), and talking points (adapted from Lyn Dawes). 3. Do fewer things better. When I first started my student teaching, it consumed my life. Go to school, plan for the next day, sleep, and repeat. I stopped exercising, watching TV, hanging out with my friends... and basically anything that was not work-related. I could've used an old lesson plan my associate teacher has taught before; I could've downloaded lesson resources online; or I could have picked one really good question and focus the class on that for the entire period. There were a million things I could have done better, but no. Instead, I scoured dozens of sites for lesson ideas, worksheets, and activities before creating my own unique cocktail using an amalgamation of the best ideas I had gathered. I made my own worksheets and presentations because I wanted things done in my own exact, particular way. Planning a single lesson would take me hours - this is not sustainable! I know better, so I'm going to do better this year. Angela Watson's keynote presentation for the Build Math Minds Virtual Summit really helped me refocus and re-evaluate my priorities. I'm going to invest my energy in doing the stuff that matters, and NOT because:
Instead I'll only commit my energy to doing something if:
Three things I'm going to start doing now to achieve this goal: 1) Manage my time by setting a timer for the tasks that need to get done, and stick to it. Whatever gets done during that time doesn't have to be perfect or have beautiful fonts and layouts, it just needs to be good enough. 2) Reduce my workload by only formally assessing student work if I believe it is a TRUE reflection of student learning. 3) Increase efficiency by delegating tasks to students, like self-marking formative assessments. |
April SooInternational math educator who writes, occasionally. Archives
April 2020
Categories
All
|

 RSS Feed
RSS Feed
